ভূ-রেখা কাকে বলে, ঊর্ধ্বরেখা কাকে বলে, উল্লম্বতল কাকে বলে, উন্নতি কোণ কাকে বলে,অবনতি কোণ কাকে বলে,∠CAD এর পরিমাণ নির্ণয় কর,AB ও BC এর দৈর্ঘ্য নির্ণয় কর,A ও D এর দূরত্ব নির্ণয় কর

প্রশ্ন সমাধান: ভূ-রেখা কাকে বলে, ঊর্ধ্বরেখা কাকে বলে, উল্লম্বতল কাকে বলে, উন্নতি কোণ কাকে বলে,অবনতি কোণ কাকে বলে,∠CAD এর পরিমাণ নির্ণয় কর,AB ও BC এর দৈর্ঘ্য নির্ণয় কর,A ও D এর দূরত্ব নির্ণয় কর

1। 150 মিটার লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে। ঘুড়িটি যদি অনুভূমিক রেখার সাথে 60∘ কোণ করে উড়তে থাকে, তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে?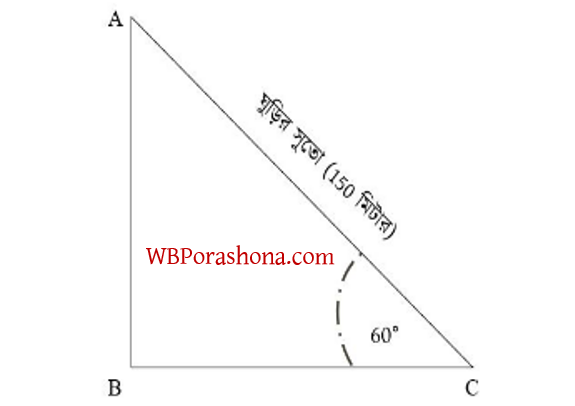

$1$
সমাধান- AC সুতোর দৈর্ঘ্য 150 মিটার
ভূমি (BC) এর সাথে ঘুড়িটির উন্নতি কোণ ∠ACB = 60∘
AB = মাঠ থেকে ঘুড়িটির উচ্চতা
△ABC থেকে পাই,
sinθ = লম্ব\ অতিভুজ
বা, sin60∘=ABAC
বা, 3√2=AB150
বা, AB=150×3√2
বা, AB=753–√
সুতরাং, ঘুড়িটি মাঠ থেকে 753–√ মিটার উঁচুতে রয়েছে।(উত্তর)

2। একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো এক বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চূড়ার উন্নতি কোণ 30∘ থেকে 60∘ হল। চিমনির উচ্চতা কত?

$2$

সমাধান- ধরি, AB হল একটি চিমনি
C বিন্দুতে উন্নতি কোণ ∠ACB=30∘
D বিন্দুতে উন্নতি কোণ ∠ADB=60∘
CD = 50 মিটার
আবার, BC = BD + CD = BD + 50 ….(i)
তাহলে △ABD থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, tan60∘=ABBD
বা, 3–√=ABBD
বা, AB=3–√BD ….(ii)
আবার △ABC থেকে পাই,
বা, tan30∘=ABBC
বা, 13√=3√BDBD+50 [(i) ও (ii) নং সমীকরণে থেকে পাই ]
বা, 3–√×3–√BD=BD+50
বা, 3BD−BD=50
বা, 2BD=50
বা, BD=25
(ii) নং সমীকরণে $BD$ এর মান বসিয়ে পাই,
AB=3–√BD=253–√
সুতরাং, চিমনির উচ্চতা 253–√ মিটার। (উত্তর)

3। উড়োজাহাজের একজন যাত্রী কোন একসময় তার এক পাশে হাওড়া স্টেশনটি এবং তার বিপরীত পাশে শহিদ মিনারটি যথাক্রমে 60∘ ও 30∘ অবনতি কোণে দেখতে পান। ওই সময়ে উড়োজাহাজটি যদি 5453–√ মিটার উঁচুতে থাকে, তাহলে হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব কত?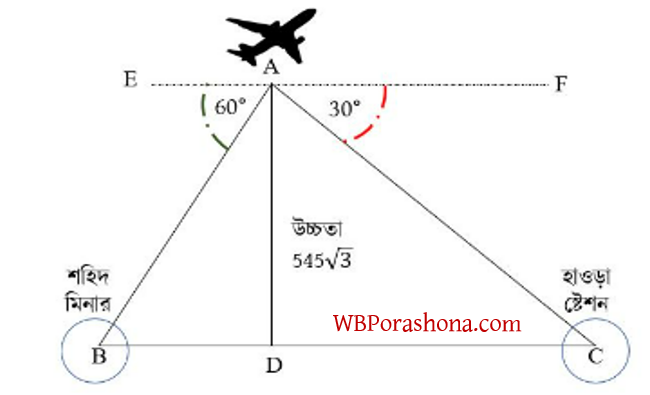

$3$

সমাধান- ধরি, A, B ও C বিন্দু তিনটি যথাক্রমে উড়োজাহাজ, শহিদ মিনার ও হাওড়া স্টেশন কে চিহ্নিত করছে।
AD হল উড়োজাহাজের উচ্চতা AD=5453–√ মিটার
অবনতি কোণ ∠EAB = 60∘ এবং ∠FAC=30∘
ধরি, BC ∥ EF
সুতরাং, ∠EAB=∠ABD=60∘ [ একান্তর কোণ ]
এবং ∠FAC=∠ACD=30∘ [ একান্তর কোণ ]
তাহলে △ABD থেকে পাই,
tanθ = লম্ব\ভূমি
বা, tan60∘=ADBD
বা, 3–√=5453√BD
বা, BD=5453√3√
বা, BD=545
আবার △ADC থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, tan30∘=ADDC
বা, 13√=5453√DC
বা, DC=5453–√×3–√
বা, DC=545×3
বা, DC=1635
BC=BD+DC=545+1635=2180
সুতরাং, হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব 2180 মিটার। (উত্তর)

4। মাঠের মাঝখানে দাঁড়িয়ে মোহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে 30∘ উন্নতি কোণে এবং 2 মিনিট পরে দক্ষিণ দিকে 60∘ উন্নতি কোণে দেখতে পেল। পাখিটি যদি একই সরল রেখা বরাবর 503–√ মিটার উঁচুতে উরে থাকে, তবে তার গতিবেগ কিলোমিটার প্রতি ঘণ্টায় কত?

সমাধান- ধরি, মোহিত A বিন্দুতে দাঁড়িয়ে উড়ন্ত পাখিটিকে প্রথমে উত্তর দিকে দেখল B বিন্দুতে এবং 2 মিনিট পর দক্ষিণ দিকে দেখল C বিন্দুতে।
পাখিটি AD=503–√ মিটার উচ্চতায় রয়েছে।
উত্তরের উন্নতি কোণ ∠BAP = 30∘
দক্ষিণের উন্নতি কোণ ∠CAQ = 60∘
∠ABD = ∠BAP = 30∘ [একান্তর কোণ ]
আবার, ∠ACD = ∠CAQ = 60∘ [একান্তর কোণ ]
△ABD থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, tan30∘=ADBD
বা, 13√=503√BD
বা, BD=503–√×3–√
বা, BD=50×3
বা, BD=150
আবার, △ACD থেকে পাই,
tan60∘=ADCD
বা, 3–√=503√CD
বা, CD=503√3√
বা, CD=50
সুতরাং, BC=BD+CD=(150+50)=200
অর্থাৎ পাখিটি 2 মিনিটে যায় 200 মিটার
পাখিটি 1 মিনিটে যায় 2002 মিটার
পাখিটি 60 মিনিটে যায় 200×602=6000 মিটার
সুতরাং, পাখিটির গতিবেগ 6 কিমি/ঘণ্টা। (উত্তর)

আরো ও সাজেশন:-

◈ ভূ-রেখা, ঊর্ধ্বরেখা এবং উল্লম্বতল :

ভূ-রেখা হচ্ছে ভূমি তলে অবস্থিত যেকোনো সরলরেখা। ঊর্ধ্বরেখা হচ্ছে ভূমি তলের উপর লম্ব যেকোনো সরলরেখা। একে উল্লম্ব রেখাও বলে।

ভূমি তলের উপর লম্বভাবে অবস্থিত পরস্পরচ্ছেদী ভূ-রেখা ও ঊর্ধ্বরেখা একটি তল নির্দিষ্ট করে। এ তলকে উল্লম্ব তল বলে।

চিত্রে : CB রেখা হচ্ছে ভূ-রেখা, BA রেখা হচ্ছে ঊর্ধ্বরেখা এবং ABC তলটি ভূমির উপর লম্ব যা উল্লম্ব তল।

◈ উন্নতি কোণ ও অবনতি কোণ :

ভূতলের উপরের কোনো বিন্দু ভূমির সমান্তরাল রেখার সাথে যে কোণ উৎপন্ন করে তাকে উন্নতি কোণ বলা হয়। O বিন্দুতে P বিন্দুর উন্নতি কোণ হচ্ছে ∠POB। ভূতলের সমান্তরাল রেখার নিচের কোনো বিন্দু ভূ-রেখার সাথে যে কোণ উৎপন্ন করে তাকে অবনতি কোণ বলা হয়। O বিন্দুতে Q বিন্দুর অবনতি কোণ হচ্ছে ∠QOA।

অনুশীলনীর প্রশ্ন ও সমাধান

প্রশ্নঃ 1 : ক. ∠CAD এর পরিমাণ নির্ণয় কর।

খ. AB ও BC এর দৈর্ঘ্য নির্ণয় কর।

গ. A ও D এর দূরত্ব নির্ণয় কর।

সমাধান :

ক. চিত্র হতে পাই, ∠ACB = 60°

∠BCD = সরলকোণ = 180°

∴ ∠ACD = 180° – ∠ACB = 180° – 60° = 120°

△ACD হতে পাই, ∠ACD + ∠ADC + ∠CAD = 180°

বা, 120° + 30° + ∠CAD = 180°

বা, ∠CAD = 180° – 150°

∴ ∠CAD = 30°

[ বি:দ্র: নমুনা উত্তর দাতা: রাকিব হোসেন সজল ©সর্বস্বত্ব সংরক্ষিত (বাংলা নিউজ এক্সপ্রেস)]

খ. △ABC এ, sin60° = লম্ব/অতিভুজ

বা, √3/2 = AB/AC = AB/20

বা, 2AB = 20√3

বা, AB = 20√3/2

∴ AB = 10√3 মিটার

= 17.320 মিটার (প্রায়)

আবার, tan60° = লম্ব/ভূমি

বা, √3 = AB/BC = 10√3/BC

বা, √3BC = 10√3

বা, BC = 10√3/√3

∴ BC = 10 মিটার

নির্ণেয় AB 17.320 মিটার (প্রায়) এবং BC 10 মিটার।

গ. মনে করি, A ও D এর দূরত্ব x মিটার অর্থাৎ, AD = x মিটার

চিত্র হতে পাই,

△ABD এ, sin³0° = লম্ব/অতিভুজ

বা, ½ = AB/AD

বা, ½ = 103/x

∴ x = 20/3

= 34.64 (প্রায়)

∴ A ও D এর দূরত্ব 34.64 মিটার (প্রায়)।

রচনা ,প্রবন্ধ	উত্তর লিংক	ভাবসম্প্রসারণ	উত্তর লিংক
আবেদন পত্র ও Application	উত্তর লিংক	অনুচ্ছেদ রচনা	উত্তর লিংক
চিঠি ও Letter	উত্তর লিংক	প্রতিবেদন	উত্তর লিংক
ইমেল ও Email	উত্তর লিংক	সারাংশ ও সারমর্ম	উত্তর লিংক

Paragraph	উত্তর লিংক	Composition	উত্তর লিংক
CV	উত্তর লিংক	Seen, Unseen	উত্তর লিংক
Essay	উত্তর লিংক	Completing Story	উত্তর লিংক
Dialog/সংলাপ	উত্তর লিংক	Short Stories/Poems/খুদেগল্প	উত্তর লিংক
অনুবাদ	উত্তর লিংক	Sentence Writing	উত্তর লিংক