লগারিদম অংক Logarithm Math থেকে নিয়োগ পরীক্ষায় আসা প্রশ্ন সমাধান, নিয়োগ পরিক্ষার জন্য ১০০% কমন লগারিদম অংক Logarithm Math এক সাথে

December 7, 2021 by Rakib Hossain Sojol

অঙ্কের ক্লাসে লগারিদমের সাথে প্রথম পরিচয়েই মনে প্রশ্ন জাগতে পারে, এই বিদ্ঘুটে ঘোরালো হিসাব-নিকাশের কীইবা প্রয়োজন? এমনিতেও গণিতে ভীতি আমাদের ছাত্র-ছাত্রীদের মনে কাঁপন ধরিয়ে দেয়। তার ওপর আছে মুখস্তবিদ্যার চর্চা, যা করতে গিয়ে কত বিনিদ্র রজনীই না নিঃশেষ হয়েছে! লগারিদমের আপাত বিদঘুটে হিসাবও মুখস্ত করতে হতো, কেন করছি, কী কাজে লাগে, তা না জেনেই। অনেক গণিতের ছাত্রকেই “লগ কি খায়, না মাথায় দেয়?” প্রশ্ন করলে তারা মাথা চুলকেও উত্তর দিতে পারবেন না।

তাই আজ আসুন লগের প্রাথমিক ধারণার পাশাপাশি এর প্রয়োজনীয়তা বা উপকারিতা সম্পর্কেও একটু জেনে নিই। প্রথমেই প্রয়োগ। লগারিদমের আবিষ্কার ঘটেছিল আজ থেকে প্রায় পাঁচশ বছর আগে, ষোড়শ ও সপ্তদশ শতাব্দীতে। সে সময়ে ছিল না কোন ক্যালকুলেটর বা কম্পিউটার। গণিতের যত হিসাব-নিকাশ, সব হাতে-কলমেই করতে হতো! এখন একবার ভাবুন তো, লক্ষ বা কোটির ঘরের সংখ্যারাজি নিয়ে যদি হিসাব করতে বসেন, তাদের গুণ-ভাগ-বর্গ-বর্গমূল করতে হয়, তাহলে কী মুসিবতে পড়বেন? দিস্তার পর দিস্তা কাগজ আর বালতি বালতি মাথার ঘাম শেষ হয়ে যাবে, সময়ের দিকে তো তাকালামই না! এই মহাঝামেলা মেটাতেই বড় বড় সংখ্যাকে ছোট করে এনে দ্রুত হিসাবের একটা নিয়ম বের করা হয়, যে নিয়মের নাম লগারিদম।

যেমন ধরুন, আমরা জানি যে y = a^x এরই অপর রূপ log (a)(y) = x [একটু ধৈর্য ধরুন, এগুলোর মানে কী তা অচিরেই ভেঙে বুঝাচ্ছি।]।

এই y = a^x ফাংশনটাকে বলে এক্সপোনেনশিয়াল ফাংশন। নিরীহদর্শন এই ফাংশনকে গণিত, পদার্থবিদ্যা, প্রকৌশলে বারবার খুঁজে পাবেন। অর্থাৎ জগতের বিভিন্ন ঘটনাতেই এই ফাংশনের দরকার আছে। কিন্তু এই ফাংশনের লগারিদম নেয়া হলে যে সরল রূপ হয়, সেটা দিয়ে হিসাব করতে অনেক সুবিধা হয়।

প্রযুক্তির উন্নতির কারণে আজকাল হয়তো সংখ্যা ইনপুট দিয়ে জটিল হিসাব মুহূর্তেই করতে পারছি, কিন্তু যদি হাতের কাছে না থাকে ক্যালকুলেটর কিংবা কম্পিউটার, যদি জীবন বিপন্ন হবার মুখে দ্রুত কোন হিসাব-নিকাশ করে বিপদ থেকে উদ্ধারের পথ থাকে, তখন বলা যায় না, এই লগারিদমই হতে পারে আপনার জীবন-মৃত্যুর সহায়! আর অমন দুর্লভ পরিস্থিতি ছাড়াও, গণিতে ভাল ধারণার জন্যেও লগের প্রয়োজন ও গুরুত্ব অনেক।

এক কথায় বললে, বড় সংখ্যার জটিল ও সময়সাপেক্ষ গুণ-ভাগকে লগের সাহায্যে ছোট ছোট যোগ বা বিয়োগে রূপান্তর করা যায়, আরও জটিল non-linear সমীকরণকে করা যায় সরলরৈখিক (linear)। তাই চলুন, লগের প্রাথমিক বিষয়গুলো জেনে নেই।

(এখান থেকে বাকি লেখাটুকু আমার। – নিপুণ সেন)

পর্ব ১

Log সম্পর্কে জানার আগে ছোটখাটো কিছু বিষয় আগে জেনে নেই চলুন।

আমরা সকলে জানি যে 2³ এর মান হলো 8।

এখানে 2 হলো ভিত্তি (base), 3 হলো ঘাত বা সূচক (power), এবং 8 হলো ফলাফল (result)। সহজ কথায়- 2 এর তৃতীয় সূচকের মান 8 বা 2 এর পাওয়ার 3 দিলে পাবো 8। এখন যদি ঘুরিয়ে বলি- 2 এর উপর ঘাত কত দিলে ফলাফল 8 হবে? হুম, এই প্রশ্নটাকেই গাণিতিকভাবে লেখা হয়ঃ

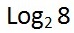
যে কোন ওয়েব ব্রাউজারে সহজে লেখার জন্য আমি Log(base)(result) এভাবে লিখেছি। এখানেও 2 হলো ভিত্তি (base), এবং 8 হল ফলাফল (result)। Log(2)(8) -এর উত্তরটা হবে 3 (power)। এবারে কিছু অনুশীলন করে নেয়া যাক, কী বলেন?

Log2 (64) অর্থাৎ 2 এর উপর পাওয়ার কত দিলে রেজাল্ট 64 হবে?
Log(2) (16) অর্থাৎ ……………?
Log(2) (256) অর্থাৎ……………..?

পর্ব ২

আচ্ছা, ভিত্তি (base) যদি 10 হয়, যেমনঃ 10² = 100, তখন হিসাবটা কেমন হবে? আগের মতই বলবো, 10 এর উপর ঘাত 2 দিলে ফলাফল হয় 100. একটু ঘুরিয়ে যদি প্রশ্ন করি – 10 এর উপর ঘাত কত দিলে ফলাফল 100 হবে? এটাই গাণিতিকভাবে- Log(10)(100) যার অর্থ 10 এর উপর পাওয়ার কত দিলে রেজাল্ট 100 হবে?

উত্তরঃ 2

সাধারণ বীজগণিতে 10-ভিত্তিক লগ-কে শুধু Log দিয়েই বোঝানো হয়। অর্থাৎ Log(10)(1000) না লিখে Log(1000) লেখা হয়।

আরো কিছু উদাহরণঃ

10^-2=0.01 ——> Log(0.01)= -2 (সাবধান কিন্তু! এটা 2 নয়। এটা -2)

10^1=10 ———–> Log(10) = 1 (এটা কিন্তু আপনার পরিচিত!)

Log(10)(10) =1—> ঐ যে, Log(a)(a) =1 সূত্র! ভিত্তি আর ফলাফল যদি একই হয়, তাহলে ঘাতের মান সবসময় হবে এক! কী মজা তাই না!

১০ এর উপর পাওয়ার কত হলে রেজাল্ট হবে ১০? সোজা উত্তরঃ ১।

তেমনিভাবে Log(2)(2)=1, Log(8)(8)=1, Log(100)(100)=1।

অনুশীলনীঃ (শূন্যস্থান পূরণ করো)

Log(1000) অর্থাৎ 10 এর উপর পাওয়ার কত দিলে রেজাল্ট 1000 হবে?
Log(0.001) অর্থাৎ……………?
Log(10) অর্থাৎ……………..?

পর্ব ৩

e একটি ধ্রুবক সংখ্যা, যার মান 2.71. এবার ভিত্তি যদি হয় e, তাহলে কী রকম হবে Log এর চেহারা?

e= 2.71

e^3=20

Log(e)(20)=3.

অর্থাৎ, e এর উপর পাওয়ার 3 দিলে ফলাফল হবে 20. সাধারণত, e-ভিত্তিক লগকে ন্যাচারাল লগ বলে এবং Ln আকারে লেখা হয়। যেমন – Log(e)(20) না লেখে Ln 20 লেখা হয়।

পর্ব ৪

শেষ বিষয়। আমরা এখন অ্যান্টি-লগ (Anti-Log) বিষয়ে জানবো। লগ আর অ্যান্টি-লগ একই মুদ্রার এপিঠ-ওপিঠ। যেমন ‘+’ আর ‘-‘ একই মুদ্রার এপিঠ – ওপিঠ। এরকম অনেক জোড়া আছে, মনে মনে চিন্তা কর। যেমন লাঙল-মই, পেন্সিল-রাবার ইত্যাদি।

এখন দেখুনঃ 100 + 5 – 5 = 100

100 এর কোন পরিবর্তন হয়েছে কী? না। ঠিক তেমনি- কোন একটা সংখ্যাকে Log করার পরে তাকে আবার Anti-Log করলে ঐ সংখ্যাটির কোন পরিবর্তন হয় না। নিচের উদাহরণটা দেখলে আরো পরিষ্কার হবে।

1000 এর 10 ভিত্তির লগ হলো- Log(1000)

এবার একে যদি 10 ভিত্তিক Anti-Log করি-

Anti-Log10 (Log(1000)) = 1000————-(1)

সহজ বাংলায় Log আর Anti-Log কাটাকুটি।

আর একটু, এই শেষ বলে।

10³ = 1000——————–(2)

তাহলে Log(1000) = 3, লিখতে পারি না? হুম, পারি।

এবার দুই পাশে 10-ভিত্তিক Anti-Log করে পাই,

=> Anti-Log(10) ( Log(1000) ) =Anti-Log(10)( 3)

=> 1000 = Anti-Log (10)( 3) [(1)নং সমীকরণ ব্যবহার করে]

=> 10^3 = Anti-Log(10)(3) [(2) নং সমীকরণ ব্যবহার করে]

=> Anti-Log(10)(3) = 10^3——————-(3)

এখানে আমরা ১০০০-এর দশভিত্তিক লগের অ্যান্টি-লগ নিচ্ছি। যেহেতু লগের মান ৩, তাই সেটার ওপরেও অ্যান্টি-লগ নেয়া হচ্ছে। বামপক্ষে লগ অ্যান্টি-লগে কাটাকাটি। রইলো শুধু ১০০০, যাকে ২ নম্বর সমীকরণ থেকে ১০^৩ লেখা যায়। তার মানে, ৩ এর ১০-ভিত্তিক অ্যান্টি-লগের মান ১০-ভিত্তির উপরে ঘাত ৩।

(3) নং সমীকরণ থেকে আমরা বলতে পারি-

একটা সংখ্যার 10-ভিত্তিক Anti-Log বলতে বুঝায় 10-এর উপর ঐ সংখ্যাটির ঘাত। তাহলে ভিত্তি যে কোন সংখ্যা হতে পারে।

3 এর e-ভিত্তিক Anti-Log বলতে বুঝায় e-এর উপর ঘাত 3।

Anti-Log(e)(3) = e^3

5 এর e-ভিত্তিক Anti-Log বলতে বুঝায় e-এর উপর ঘাত 5।

Anti-Log(e)(5) = e^5

6 এর 2-ভিত্তিক Anti-Log বলতে বুঝায় 2 এর উপর ঘাত 6।

Anti-Log(2)(6) = 2^6

4 এর 2 ভিত্তিক Anti-Log বলতে বুঝায় 2 এর উপর ঘাত 4।

Anti-Log(2)(4) = 2^4

এবার আপনি বলুন-

2 এর 8-ভিত্তিক Anti-Log বলতে বুঝায় ……………………………।

5 এর 16-ভিত্তিক Anti-Log বলতে বুঝায় ……………………………………..।

লগারিদম (Logarithm)

ভূমিকা ( Introduction )

          আমরা দেখেছি যদি a ও xবাস্তব রাশি হয় তাহলে ax(a≠0)  রাশির a কে নিধান এবং xকে ঘাতের সূচক বা শুধু ঘাত বলে। মনে করি ax=m(m>0) তাহলে a ও xএর মান জানা থাকলে আমরা  mএর মান জানতে পারি। উদাহরণস্বরূপ 52=m⇒m=25 , আবার m ও xএর মান জানা থাকলে আমরা a মান জাতে পারি। উদাহরণস্বরূপ a5=32⇒a=2 , কিন্তু a ও mএর মান জানা থাকলে আমরা সবসময় xএর মান জানতে পারিনা যেমন 4x=16⇒x=2,3x=16 এখানে প্রথম উদাহরণের ক্ষেত্রে xএর মান জানতে পারি কিন্তু দ্বিতীয় উদাহরণের ক্ষেত্রে xএর মান জানতে পারছিনা।বীজগণিতের যে বিশেষ পদ্ধতিতে ax=m সম্পর্ক থেকে xএর মান পাওয়া যায় তাকে লগারিদম বলে।

 

লগারিদমের সংজ্ঞা(Definition of Logarithm)

ax=m(a>0,m>0,a≠1) হলে x কে a নিধানের সাপেক্ষে mসংখ্যাটির লগারিদম বলে। x=logam এই আকারে লগারিদম প্রকাশ করা হয়।

x=logam কে বলা হয় “x is a logarithm  of m to the base a”

অতএব ax=m⇒x=logam
দৃষ্টান্ত

·         নিধান না জানা থাকলে কোনো সংখ্যার লগারিদম সম্ভব নয়।

·         কোনো সংখ্যার লগারিদমের মান নির্দীষ্ট নয় তা নিধানের উপর নির্ভর করে।

·         যদি m<0 হয় তবে xএর মান অবাস্তব।

ধনাত্মক যেকোনো নিধান a(a≠0)  সাপেক্ষে 1এর লগারদমের মান শূন্য হবে।

আমরা জানি a0=1(a≠0)⇒loga1=0
যদি নিধান ও সংখ্যা উভয়েই ধনাত্মক এবং পরস্পর সমান হয় তবে সংখ্যাটির লগারিদমেন মান সর্বদা 1হবে।

প্রমান: a=m⇒ax=a⇒x=logaa=1
 

যদি x=logam হয় তবে alogam=m হবে।

প্রমান: x=logam⇒ax=m⇒alogam=m
লগারিদমের সাধারণ সূত্রাবলি(General laws of logarithm)

1.       loga(mn)=logam+logan
2.       loga(mn)=logam−logan
3.       logamp=plogam
4.       logam=logbm×logab
যেখানে m,n,a,b>0,a≠1,b≠1,p যেকোনো বাস্তব রাশি।

সূত্রবলিরপ্রমাণ(Proof of laws)

1.       loga(mn)=logam+logan
মনে করি

ax=m→(1)⇒x=logam→(2)ay=n→(3)⇒y=logan→(4)
(1)⋅(3) করে পাই

ax⋅ay=mn⇒ax+y=mn⇒x+y=loga(mn)⇒loga(mn)=x+y⇒loga(mn)=logam+logan
[(2) ও (4)থেকে পাই]

2.       loga(mn)=logam−logan
মনে করি

ax=m→(1)⇒x=logam→(2)ay=n→(3)⇒y=logan→(4)
(1)(3) করে পাই

axay=mn⇒ax−y=mn⇒x−y=loga(mn)⇒loga(mn)=logam−logan
        [(2) ও (4)থেকে পাই]

 

3.       logamp=plogam
মনে করি

 x=logam→(1)⇒ax=m→(2)y=logamp→(3)⇒ay=mp→(4)
(2)ও(4)থেকে পাই

ay=mp⇒ay=(ax)p⇒ay=axp⇒y=xp⇒logamp=plogam
অনুসিদ্ধান্ত: logam−−√n=logam1n=1nlogam
4.       logam=logbm×logab
মনে করি

x=logam⇒ax=m→(1)y=logbm⇒by=m→(2)z=logab⇒az=b→(3)
অতএব

ax=by[(1),(2)]⇒ax=(az)y[(3)]⇒ax=azy⇒x=zy⇒logam=logab×logbm[(1),(2),(3)]
অনুসিদ্ধান্ত:

 logab×logba=1⇒logab=1logba
আবার আমরা প্রমান করতে পারি logbm=logamlogab
 

 

 

 

 

সংক্ষিপ্তকরণ(Summarisation)

m,n,a,b>0,a≠1,b≠1,p যেকোনো বাস্তব রাশি হলে,

1.    loga1=0
2.   logaa=1
3.   alogam=m
4.   loga(mn)=logam+logan
5.   loga(mn)=logam−logan
6.   logamp=plogam
7.   logam=logbm×logab
8.   logab×logba=1
9.   logba=1logab
10.   logbm=logamlogab
 

 

উদাহরণ ১৷

প্রমান করো  7log109+3log8180=2log2524+log2   [H.S '82]

প্রমান:

7log109+3log8180=7(log10−log9)+3(log81−log80)=7log10+3log81−(7log9+3log80)=7log(2×5)+3log34−7log32−3log(24×5)=7log2+7log5+12log3−14log3−12log2−3log5=−5log2−2log3+4log5=2log52+log2−6log2−2log3=2log25−2log23−2log3+log2=2log258×3+log2=2log2524+log2(proved)
 

 

 

উদাহরণ ২৷

প্রমান করো  log210−log8125=1[H.S '90]

প্রমান:

log210−log8125=log2(2×5)−log853=log22+log25−3log85=1+log25−31log58=1+log25−31log523=1+log25−313log52=1+log25−1log52=1+log25−log25=1(proved)
 

 

উদাহরণ ৩৷

যদি logxy−z=logyz−x=logzx−y হয় তবে দেখাও যে xxyyzz=1[H.S'2000]

প্রমান:

ধরি

logxy−z=logyz−x=logzx−y=klogx=k(y−z),logy=k(z−x),logz=k(x−y)
xlogx=xk(y−z)⇒logxx=k(xy−xz)→(1)ylogy=yk(z−x)⇒logyy=k(zy−xy)→(2)zlogz=zk(x−y)⇒logzz=k(xz−yz)→(3)(1)+(2)+(3)logxx+logyy+logzz=k(xy−xz+yz−yx+xz−yz)⇒logxxyyzz=k×0⇒logxxyyzz=0⇒xxyyzz=1(proved)
 

 

উদাহরণ ৪৷

সমাধান করো: logx2⋅logx162=logx642 [H.S'95,Jt Ent'81]

সমাধান:

logx2⋅logx162=logx642⇒logx2⋅1log2x16=1log2x64⇒logx2⋅log2x64=log2x16⇒logx2(log2x−log264)=log2x−log216⇒logx2⋅log2x−logx2⋅log226=log2x−log224⇒1−logx2⋅6log22=log2x−4log22⇒1−6logx2=log2x−4⇒6logx2=5−log2x⇒61log2x=5−log2x⇒5log2x−(log2x)2=6⇒(log2x)2−5log2x+6=0⇒a2−5a+6=0[log2x=a]⇒(a−3)(a−2)=0a=3⇒log2x=3⇒x=23=8or,a=2⇒log2x=2⇒x=22=4

(BCS প্রিলিমিনারিতে সূচক ও লগারিদম, সমান্তর ও গুণোত্তর অনুক্রম ও ধারা থেকে সর্বোচ্চ ০৩ নম্বর থাকবে এবং অন্যান্য প্রতিযোগিতামূলক পরীক্ষায়ও এ অধ্যায়গুলো থেকে প্রশ্ন থাকে)

পাওয়ারের বিপরীত তত্ত্ব হচ্ছে লগারিদম। যেমন দেখুনঃ

23 =2 x 2 x 2 =8

লগারিদমে এটিকে প্রকাশ করা হয়, log2 8 = 3. যেখানে 2 হল লগের বেইস, 8 হল লগের পাওয়ার।

23=8 —> log2 8 = 3; পাওয়ার ডান পাশে চলে আসবে।

20=1 —> log2 1 = 0

51=5 —> log5 5 = 1

শুধু ধনাত্মক সংখ্যারই লগারিদম আছে, শূন্য বা ঋণাত্মক সংখ্যার লগারিদম নেই।

লগারিদম-সম্পর্কিত মৌলিক কিছু বিষয়:
(i) লগের সংজ্ঞানুসারে loga1 = 0 বা সাধারণভাবে log1=0 অর্থাৎ যেকোনো ভিত্তিতে লগের পাওয়ার 1 হলে তার মান শূন্য হয়।
(ii) লগের সংজ্ঞানুসারে logaa = 1 অর্থাৎ লগের ভিত্তি এবং লগের পাওয়ার একই হলে তার মান 1 হয়।
(iii) একই ভিত্তির সাপেক্ষে দুই বা ততোধিক সংখ্যার গুণফলের লগারিদম ওই একই ভিত্তির ওপর সংখ্যাগুলোর পৃথক পৃথক লগারিদমের সমষ্টির সমান,
অর্থাৎ, loga(M´N) = logaM+logaN এবং
(iv) একই ভিত্তির সাপেক্ষে দুটি সংখ্যার ভাগফলের লগারিদম, ওই একই ভিত্তির ওপর সংখ্যা দুটির পৃথক পৃথক লগারিদমের বিয়োগফলের সমান,
অর্থাৎ, loga(M÷N) বা loga M/N = logam – logaN
(v) সূচকযুক্ত সংখ্যার লগারিদম, ওই সূচক ও ওই সংখ্যার লগারিদমের গুণফলের সমান অর্থাৎ logaMr = rlogaM

(vi) যদি লগের বেইস উল্ল্যেখ না থাকে তবে ধরে নিতে হবে প্রদত্ত অংকে সব লগারিদমের বেইস সমান।

কিছু সমাধানঃ

log28=কত?

log28 = log223

এখন সূচকযুক্ত সংখ্যার লগারিদম, ওই সূচক ও ওই সংখ্যার লগারিদমের গুণফলের সমান অর্থাৎ logaMr = rlogaM

তারমানে log223 = 3 log22

লগের সংজ্ঞানুসারে logaa = 1 অর্থাৎ লগের ভিত্তি এবং লগের পাওয়ার একই হলে তার মান 1 হয়।

অর্থাৎ 3 log22 = 3×1 = 3

log2(1/32) এর মান-

log 2(1/25) = log22-5= -5 log22 = -5×1 = -5

অংক নতুন

১) লগ(log) হচ্ছে এমন একটি অপারেটর যার কাজ অনেক বড় বড় সংখ্যাকে ছোট করে দেয়া। আর লগের এই ছোট মান দ্বারা সেই বড় মানটি বের করে ফেলা সম্ভব। যেমনঃ একটি সংখ্যা ১,০০,০০,০০০ ধরে নেয়া যাক। এখন আমরা ১০ ভিত্তিক একটি লগ নিলাম এবং আমাদের সংখ্যাটিকে সেই ১০ ভিত্তিক লগের ভেতর ফেলে দিলাম। তাহলে, আমাদের মান আসবে মাত্র ৭!

PEXmB0x8QD ld5zWde3 zrtXxhupwZdUNCD7LFSNXUwx 2dlKmYzCdWSGAKivrpJj0ykFWa9LAThBrFsuYZQz8Ee haCks9B02ALd4j8osNiCsevYwkK0uUrV fQBJ

(২) “লগের ভিত্তি” বা “লগের বেইজ” ছাড়া কিন্তু লগ কখনই কাজ করতে পারে না। তাই প্রতিটা লগে অবশ্যই এর ভিত্তি বলে দেয়া থাকতে হবে। আর এই ভিত্তি থাকে log এর g অক্ষরের গোঁড়ায়। যা লগের বেইজ লেখার স্ট্যান্ডার্ড ফর্ম। লগের বেইজ লেখা শেষ। এবার যেই সংখ্যাকে আমরা ছোট করতে চাই, সেই সংখ্যাকে লিখতে হবে “লগের বেইজ” এর ঠিক উপরে। যেইভাবে আমরা সাধারণত কোন সংখ্যার উপর “power” বা “to the power” বা “ঘাত” লিখে থাকি সেইভাবে।

s7mBACrh1YvZMWi0PqSAukVD9bvc2lO1Pnerx2Y8PWXgNgcXhgyMpdG7Ke1KlD

(৩) লগ সর্বদা “power” বা “to the power” বা “ঘাত” নিয়ে কাজ করে। আর ‘লগের ভিত্তি’ বা ‘লগের বেইজ’ মূলত সেই কাজটি পরিচালনা করে থাকে।

(৪) কোন লগারিদম বা লগের অংকে input এ একটি সংখ্যা দেয়া হয়। লগের কাজ হল সেই সংখ্যাকে লগের বেইজ এর “power”হিসেবে প্রকাশ করা। যা হচ্ছে ঐ লগের ফলাফল। অর্থাৎ, লগের ফলাফল হচ্ছে বেইজ এর “power” বা”ঘাত”।

যেমনঃ প্রথমে আমরা ১,০০,০০,০০০ সংখ্যাটি input হিসেবে ধরে নিয়েছিলাম এবং লগের ভিত্তি বা বেইজ হিসেবে নিয়েছিলাম ১০ কে। যার ফলে এই লগের ফলাফল আসে ৭. এখন একটু লক্ষ্য করা যাক। আমরা যেই সংখ্যা নিয়েছিলাম সেখানে শুন্য ছিল ৭ টি। আবার, লগের ভিত্তি হিসেবে নেয়া ১০ এর “power” বা “to the power” বা “ঘাত” যদি ৭ হয়, তবে তার মান হয় ১,০০,০০,০০০. অর্থাৎ, কোন সংখ্যাকে যদি ১০ ভিত্তিক একটি লগের মেশিনের মধ্যে ফেলা হয়, তাহলে সেই লগের মেশিন ঐ সংখ্যাটিকে ১০ এর “power” বা “to the power” বা “ঘাত” হিসেবে তৈরি করবে এবং তা ফলাফল হিসেবে প্রদর্শন করবে।

★★★এইভাবে কোন বড় সংখ্যাকে লগের মাধ্যমে ছোট করে ফেলা সম্ভব।

(৫) বাস্তব জীবনে লগের ব্যবহার

বাস্তবে আমরা অনেক কাজেই লগ ব্যবহার করে থাকি। যেমনঃ

(১) ভূমিকম্প মাপার মেশিনের নাম হচ্ছে “Richter magnitude scale” বা আমরা শুধু “রিক্টার স্কেল” বলে থাকি। এই স্কেল মূলত ১০ ভিত্তির লগ নিয়ে কাজ করে। রিক্টার স্কেল যখন ভূমিকম্পের মাত্রা ৬ দেখায়, তখন এর মান হচ্ছে 10⁶. অর্থাৎ, ১০০০০০০. আবার যখন এই স্কেলে ভূমিকম্পের মাত্রা ৭ দেখায়, তখন এর মান হচ্ছে 10⁷. অর্থাৎ, ১০০০০০০০. দেখা যাচ্ছে, ১০ ভিত্তিক লগের মান ১ বেড়ে গেলে, এর মান আসলে ১ বাড়ে না। এর মান বেড়ে যায় ১০ গুণ!

(২) শব্দের তীব্রতা মাপার একক ডেসিবেলও লগারিদম ব্যবহার করে হিসাব করা হয়। কারণ হলো, বড় পরিবর্তনকে ছোট আকারে প্রকাশ করা।

(৩) পানির অম্লত্ব পরিমাপের একক pH নির্ণয়েও রয়েছে লগারিদমের ব্যবহার। এটি মূলত হিসাব করা হয় প্রতি লিটার পানিতে কত সংখ্যক ধনাত্মক হাইড্রোজেন আয়ন রয়েছে। এর মান 0.0000001 থেকে প্রায় 1 পর্যন্ত হতে পারে। মানের এই বিশাল পরিবর্তন মনে রাখা বেশ কঠিন তো, তাই লগ ব্যবহার করে এই সীমাকে 0 থেকে 7 এর মধ্যে নামিয়ে আনা হয়েছে। 0 থেকে 7 এর মধ্যে একটা সংখ্যা মনে রাখা সহজ।

(৬) লগারিদমের ভিত্তি যা খুশি হতে পারে। এর কোন বাধা ধরা নিয়ম নেই। তবে, নির্দিষ্ট কিছু ভিত্তি বেশি ব্যবহার করা হয়। তার মধ্যে সবার আগে আসে 10. সাধারণভাবে এটিই সবচেয়ে বেশি ব্যবহার করা হয়। আমাদের ক্যালকুলেটরে সাধারণত যেই log থাকে সেটার ভিত্তি দশ। যদি, লগের ভিত্তি লেখা না থাকে, তাহলে ধরে নিতে হয় এর ভিত্তি হচ্ছে 10

(৭) লগারিদমের মূল ব্যবহার হচ্ছে বড় সংখ্যাকে ছোট আকারে প্রকাশ করা ।

(৮) Sentence making=tens, right form of verb,sub verb agreement, vocabulary.

(৯) বীজগণিতের যে বিশেষ পদ্ধতিতে a^x=M সম্পর্ক থেকে xএর মান পাওয়া যায় তাকে লগারিদম বলে।

যেমন 4^x=16⇒x=2

আর লগারিদম প্রকাশ করা হয় x=loga^M এই আকারে।

(১০) নিধান বা ভিত্তি জানা না থাকলে কোনো সংখ্যার লগারিদম সম্ভব নয়।

(১১) কোনো সংখ্যার লগারিদমের মান নির্দিষ্ট নয় তা ভিত্তির/নিধানের উপর নির্ভর করে।

(১২) log₂8=3 এখানে (লগে) আমরা ৩ টা সংখ্যাকে নিয়ে কাজ করছি ।

(1) base , যে সংখ্যার ওপর আমরা power বসাতে চাই । (উদাহরণে 2 )

(2) base এর ওপর যত power বসাতে চাই (উদাহরণে 3 বার , এই 3 ই হচ্ছে লগারিদম )

(3) base এর ওপর power বসিয়ে যে সংখ্যাটি আমরা পেতে চাই (ওপরের উদাহরণে 8 )

(১৩) পাওয়ারের বিপরীত তত্ত্ব হচ্ছে লগারিদম। যেমন দেখুনঃ

2³=2 x 2 x 2 =8

লগারিদমে এটিকে প্রকাশ করা হয়, log₂8 = 3. যেখানে 2 হল লগের বেইস, 8 হল লগের

পাওয়ার।

(১৪) শুধু ধনাত্মক সংখ্যারই লগারিদম আছে, শূন্য বা ঋণাত্মক সংখ্যার লগারিদম নেই।

(১৫) লগারিদম-সম্পর্কিত মৌলিক কিছু বিষয়:

(i) যেকোনো ভিত্তিতে লগের পাওয়ার 1 হলে তার মান শূন্য হয়।যেমনঃ log_a1= 0

(ii) লগের ভিত্তি এবং লগের পাওয়ার একই হলে তার মান 1 হয়।যেমনঃ log_aa = 1

(iii) একই ভিত্তির সাপেক্ষে দুই বা ততোধিক সংখ্যার গুণফলের লগারিদম ওই একই ভিত্তির ওপর সংখ্যাগুলোর পৃথক পৃথক লগারিদমের সমষ্টির সমান।যেমনঃ

log_a(MN) = log_aM+log_aN

(iv) একই ভিত্তির সাপেক্ষে দুটি সংখ্যার ভাগফলের লগারিদম ওই একই ভিত্তির ওপর সংখ্যা দুটির পৃথক পৃথক লগারিদমের বিয়োগফলের সমান।যেমনঃ

log_a(M÷N) বা log_a

= log_aM – log_aN

(v) সূচকযুক্ত সংখ্যার লগারিদম, ওই সূচক ও ওই সংখ্যার লগারিদমের গুণফলের সমান।

যেমনঃ log_aM^r = rlog_aM অর্থাৎ,log₂2³= 3log₂2 = 3×1= 3

(vi) যদি লগের বেইস উল্লেখ না থাকে তবে ধরে নিতে হবে প্রদত্ত অংকে সব লগারিদমের বেইস সমান।

(১৬) e ভিত্তিক লগ। e একটি অমূলদ সংখ্যা। এর মান প্রায় 2.71828. মূলত, প্রকৌশল বিদ্যায় e ভিত্তিক লগের ব্যবহার বেশি। একে ন্যাচারাল লগারিদম বলা হয় এবং ln দিয়ে প্রকাশ করা হয়। ln দ্বারা বোঝায় কোন সংখ্যার e ভিত্তিক লগ।

(১৭) কম্পিউটার বিজ্ঞানে এবং ইলেকট্রনিক্সে 2 ভিত্তিক লগের প্রচুর ব্যবহার রয়েছে।

(১৮) ভিত্তি যাই হোক না কেন, তার ঘাত শূন্য হলেই মান 1 হবে।

সূত্র ১। log_aa = 1

সূত্র ২। log_a1 = 0

সূত্র ৩। log_aaM = M

সূত্র ৪। log_a(MN) = log_aM + log_aN

সূত্র ৫। log_a

= log_aM – log_aN

সূত্র ৬। log_aMⁿ = nlog_aM

সূত্র ৭। log_aM = log_ab×log_bM অথবা log_bM× log_ab

সূত্র ৮। log_ab = 1/log_ba

সূত্র ৯। যদি, a^x=M হয়, তবে x = log_aM

(১৯) বিভিন্ন প্রকার লগারিদমঃ

Logarithm এর বেস ১০ হলে একে বলা হয় ১০ ভিত্তিক লগারিদম, বেস ২ হলে একে বলা হয় ২ ভিত্তিক লগারিদম। আর বেস e (e একটি অমূলদ সংখ্যা। এর মান হল 2.7182818284….) হলে একে বলা হয় ন্যাচারাল লগারিদম। একে বেশীরভাগ ক্ষেত্রে log না লিখে ln লিখা হয়।

(২০) 10 ভিত্তিক লগারিদম সাধারণ দশমিক সংখ্যা পদ্ধতির হিসাবে ব্যবহার করা হয়। এটা দিয়ে আপনি বুঝতে পারবেন কোন সংখ্যাকে 10 দিয়ে সর্বোচ্চ কতবার নিঃশেষে ভাগ করা যায়।

যেমনঃ log₁₀(1000)=3

এটার থেকে আপনি বুঝতে পারেন 1000 কে 10 দিয়ে সর্বোচ্চ তিনবার নিঃশেষে ভাগ করা যায়।আমরা দৈনন্দিন কাজে দশমিক সংখ্যা পদ্ধতি ব্যবহার করি তাই সাধারণ হিসাবে ১০ ভিত্তিক লগারিদম যথেষ্ট।

★আবার ডিজিটাল ডিভাইস বা কম্পিউটার বাইনারি সংখ্যা পদ্ধতিতে কাজ করে যার ভিত্তি ২। এজন্য কম্পিউটার প্রকৌশলে ২ ভিত্তিক লগারিদমের ব্যবহার প্রায় সবক্ষেত্রেই দেখা যায়।

(২১) সংজ্ঞা:লগারিদম হল একটি অপারেটর যা অন্য দুইটি সংখ্যা ব্যবহার করে অন্য আরেকটি সংখ্যা(সূচক) জানায়।

ব্যাখ্যা:প্রথম দুইটি সংখ্যার একটি হল ভিত্তি (বেস, যার মান 1 হবে না) যার উপরে অন্য সংখ্যাটির (ধনাত্মক সংখ্যা,শূন্য ব্যতীত)লগারিদমের মান বের করা হয়।

★লগারিদম হলো সূচক প্রক্রিয়ার বিপরীত। যেমন গুণ এবং ভাগ প্রক্রিয়া একে অপরের বিপরীত।

সংক্ষিপ্ত সংজ্ঞা:কোন একটি সংখ্যার (শূন্যের চেয়ে বড়) লগারিদম (ভিত্তির সাপেক্ষে) হলো এমন একটি সংখ্যা(সূচক),যাকে ভিত্তির ঘাত (পাওয়ার) হিসেবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়।

যেমন:

(২২) একটা গুরুত্বপূর্ণ বিষয় হল, শর্ত কিন্তু শুধু ভিত্তির(base) জন্য; সূচকের জন্য কোন শর্ত নেই।(s)

(২৩) একটা গুরুত্বপূর্ণ ব্যাপার হলো,লগারিদম ফাংশনে একটা শর্ত জুড়ে দেয়া আছে। কিন্তু সুচকীয় ফাংশনে কোন শর্ত নেই।

★★শর্তানুযায়ী লগারিদমের ভিত্তি (base) কখনও

ঋণাত্মক হতে পারে না, 1 ও হতে পারে না।

(২৪) গণনা সহজ করার জন্য সপ্তদশ শতাব্দীর শুরুর দিকে জন নেপিয়ার লগারিদম এর সূচনা করেন। স্লাইড রুল এবং লগ সারণি ব্যবহার করে সহজে গণনার জন্য নাবিক, বৈজ্ঞানিক, প্রকৌশলী এবং অন্যান্যরা খুব দ্রুতই এগুলো গ্রহণ করেন। বিরক্তিকর বহুসাংখ্যিক গুণনের ধাপসমূহ লগারিদমের নিয়মে একটি সরল যোগে পরিণত হয়। লগারিদমের নিয়মানুযায়ী সংখ্যাসমূহের গুণফলের লগারিদম এর মান সংখ্যাগুলোর একক লগারিদমের মানের যোগফল। অর্থাৎ, log_b(xy) = log_b(x) + log_b(y)

(২৫) সূচক, ভিত্তি ও সূচকীয় রাশি কী?

কোনো রাশিতে একই উৎপাদক যতবার গুণ আকারে থাকে তাকে ঐ উৎপাদকের সূচক বলে। আর উৎপাদকটিকে ভিত্তি বলে। যেমন:

8= 2 x 2 x 2 = 2³

এখানে, 2 উৎপাদকটি 3 বার আছে। সুতরাং, সূচক বা ঘাত = 3, ভিত্তি = 2, সূচকীয় রাশি = 2³

আবার,

a x a x a x a x a = a⁵

এখানে, a উৎপাদকটি 5 বার আছে। সুতরাং, সূচক বা ঘাত = 5, ভিত্তি = a, সূচকীয় রাশি = a⁵

সুচক শূন্য হলে কী হবে?

কোন ভিত্তির সূচক শূন্য হলে তা 1 এর সমান হবে।

যেমন, 7⁰ = 1

সূচকের মান নির্ণয় করি:

কোন ভিত্তিকে সেই সংখ্যা দিয়েই কতবার গুণ

করতে হবে সূচক তা নির্দেশ করে।

উদাহরণ অনুযায়ী, 4³ দ্বারা বোঝা যায় ভিত্তি 4

কে তার নিজের সাথে 3 বার গুণ করতে হবে:

4³ = 4 x 4 x 4

= 64

(২৬) সূচক মূলত গুণের পুনরাবৃত্তি।

(২৭) গণিতের ক্ষেত্রে লগারিদম হলো সূচকের বিপরীত প্রক্রিয়া। এর অর্থ কোনো সংখ্যার লগারিদম হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের, (ভিত্তির) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়।

সাধারণ ক্ষেত্রে লগারিদম একটি সংখ্যা (ভিত্তি)কতবার গুণ করা হলো সেটা গণনা করে। যেমন, ১০০০ এর ১০ ভিত্তিক লগের মান ৩, এর অর্থ হলো ১০ এর ঘাত ৩ এ উন্নীত করলে ১০০০ পাওয়া যায় (১০০০ = ১০ x ১০ x ১০ = ১০^৩)। এখানে ১০ সংখ্যাটি ৩ বার গুণ করলে ১০০০ পাওয়া যায়।

আরও সাধারণভাবে বলা যায়,কোনো ধনাত্মক প্রকৃত সংখ্যাকে কোনো প্রকৃত ঘাতে উন্নীত করলে সবসময় ধনাত্মক ফল পাওয়া যায়।

১ম থেকে ৪৩তম বিসিএস প্রশ্ন ও সমাধান লিংক

Professor Primary Assistant Teacher book লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

ইংরেজি

ইংরেজি ব্যাকরণ

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
Parts of Speech	প্রশ্ন ও উত্তর লিংক	Abbreviations or Elaboration Terms	প্রশ্ন ও উত্তর লিংক
Article	প্রশ্ন ও উত্তর লিংক	One word Substitutions	প্রশ্ন ও উত্তর লিংক
Appropriate Preposition	প্রশ্ন ও উত্তর লিংক	English literature	প্রশ্ন ও উত্তর লিংক
Preposition	প্রশ্ন ও উত্তর লিংক	Sentence Correction	প্রশ্ন ও উত্তর লিংক
Right forms of verb	প্রশ্ন ও উত্তর লিংক	Translation /Vocabulary	প্রশ্ন ও উত্তর লিংক
Voice	প্রশ্ন ও উত্তর লিংক	Spelling	প্রশ্ন ও উত্তর লিংক
Narration	প্রশ্ন ও উত্তর লিংক	Synonym-Antonym	প্রশ্ন ও উত্তর লিংক
Phrase and Idioms	প্রশ্ন ও উত্তর লিংক	Word Meaning	প্রশ্ন ও উত্তর লিংক
prefix and suffix	প্রশ্ন ও উত্তর লিংক	প্রায় ৩০০টি প্রশ্ন উত্তরসহ	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

বাংলা

বিগত ৩০ বছরে বাংলা সাহিত্য ও ব্যাকরণ নিয়োগ পরীক্ষায় আষার সকল MCQ নৈবিত্তিক প্রশ্ন সমাধান এক সাথে, নিয়োগ পরীক্ষায় বাংলা থেকে আসা প্রশ্নগুলোর সমাধান প্রশ্ন ও উত্তর লিংক

বাংলা ব্যাকরণ

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
সন্ধি	প্রশ্ন ও উত্তর লিংক	শেখ হাসিনা	প্রশ্ন ও উত্তর লিংক
বিপরীত শব্দ	প্রশ্ন ও উত্তর লিংক	বঙ্গবন্ধু শেখ মজিবুর রহমান	প্রশ্ন ও উত্তর লিংক
সমার্থক শব্দ	প্রশ্ন ও উত্তর লিংক	জাতীর ৪ নেতা	প্রশ্ন ও উত্তর লিংক
শুদ্ধ বানান	প্রশ্ন ও উত্তর লিংক	বিভিন্ন চুক্তি বাংলাদেশের সাথে ভারতের সীমান্ত	প্রশ্ন ও উত্তর লিংক
এককথায় প্রকাশ	প্রশ্ন ও উত্তর লিংক	মুক্তিযুদ্ধ সেক্টর	প্রশ্ন ও উত্তর লিংক
তৎসম অর্ধতৎসম তদ্ভব বিদেশী ও দেশি শব্দ	প্রশ্ন ও উত্তর লিংক	রােহিঙ্গা সমস্যা	প্রশ্ন ও উত্তর লিংক
উপসর্গ	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের জনপদ	প্রশ্ন ও উত্তর লিংক
সমাস	প্রশ্ন ও উত্তর লিংক	সংবিধান	প্রশ্ন ও উত্তর লিংক
বাগধারা, প্রবাদ ও প্রবচন	প্রশ্ন ও উত্তর লিংক	মুক্তিযুদ্ধ	প্রশ্ন ও উত্তর লিংক
কারক-বিভক্তি	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের ভৌগলিক	প্রশ্ন ও উত্তর লিংক
যুক্ত বর্ণের	প্রশ্ন ও উত্তর লিংক	কবি সাহিত্যিকের রচনা বা জন্ম মৃত্যু	প্রশ্ন ও উত্তর লিংক
ধ্বনি, বর্ণ	প্রশ্ন ও উত্তর লিংক	উপন্যাস/রচনাসমগ্র	প্রশ্ন ও উত্তর লিংক
বাক্য (সরল, জটিল, যৌগিক)	প্রশ্ন ও উত্তর লিংক	ভাষা আন্দোল	প্রশ্ন ও উত্তর লিংক
পদ নির্ণয়	প্রশ্ন ও উত্তর লিংক	বিখ্যাত স্থান	প্রশ্ন ও উত্তর লিংক
দ্বিরুক্ত শব্দ/ দ্বন্দ্ব	প্রশ্ন ও উত্তর লিংক	স্বাধীন বাংলাদেশের অভ্যুদয়ের ইতিহাস	প্রশ্ন ও উত্তর লিংক
বাংলাদেশের চলচ্চিত্র	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের কৃষ্টি ও সংস্কৃতি প্রত্নতাত্ত্বিক নিদর্শন	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

গণিত

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
*দশমিকের (যোগ, বিয়োগ, গুণ, ভাগ)**	প্রশ্ন ও উত্তর লিংক	বীজগাণিতিক মান নির্ণয়	প্রশ্ন ও উত্তর লিংক
শতকরা, লাভ-ক্ষতি, মুনাফা	প্রশ্ন ও উত্তর লিংক	উৎপাদক নির্ণয়, গড়, মধ্যক, প্রচুরক নির্ণয়	প্রশ্ন ও উত্তর লিংক
ল.সা.গু, গ.সা.গু	প্রশ্ন ও উত্তর লিংক	ত্রিভুজক্ষেত্র, বর্গক্ষেত্র	প্রশ্ন ও উত্তর লিংক
ঐকিক নিয়ম (কাজ, খাদ্য, সৈন্য)	প্রশ্ন ও উত্তর লিংক	আয়তক্ষেত্রের বেসিক সূত্রের অংকসমূহ, সরলরেখা	প্রশ্ন ও উত্তর লিংক
অনুপাত:সমানুপাত	প্রশ্ন ও উত্তর লিংক	গাছের উচ্চতা/ মিনারের উচ্চতা	প্রশ্ন ও উত্তর লিংক
সংখ্যা পদ্ধতি	প্রশ্ন ও উত্তর লিংক	মইয়ের দৈর্ঘ্য/সূর্যের উন্নতি	প্রশ্ন ও উত্তর লিংক
বিগত সালে প্রশ্ন	প্রশ্ন ও উত্তর লিংক	পরিমাপ ও পরিমান	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

কম্পিউটার

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
তথ্য ও প্রযুক্তি লিখিত প্রশ্ন উত্তর	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের তথ্য ও যোগাযোগ প্রযুক্তি	প্রশ্ন ও উত্তর লিংক
কম্পিউটার	প্রশ্ন ও উত্তর লিংক	সেটেলাইট-১	প্রশ্ন ও উত্তর লিংক
LAN, WAN কম্পিউটার নেটওয়ার্ক	প্রশ্ন ও উত্তর লিংক	কম্পিউটার সংক্ষিপ্ত শব্দের পূর্ণরুপ	প্রশ্ন ও উত্তর লিংক
গুগল	প্রশ্ন ও উত্তর লিংক	বিভিন্ন দেশের ইন্টারনেট স্পীড	প্রশ্ন ও উত্তর লিংক
৩জি,৪জি, ৫ জি	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

General Knowledge (GK) সাধারণ জ্ঞান ও বিজ্ঞান

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
ইতিহাস , সভ্যতা ও সংস্কৃতি	প্রশ্ন ও উত্তর লিংক	পুরস্কার ও সম্মাননা	প্রশ্ন ও উত্তর লিংক
গভর্নর জেনারেল ও ভাইসরয়দের তালিকা	প্রশ্ন ও উত্তর লিংক	খেলাধুলা	প্রশ্ন ও উত্তর লিংক
বাংলার শাসন আমল	প্রশ্ন ও উত্তর লিংক	জিন-কোষ	প্রশ্ন ও উত্তর লিংক
ভূপ্রকৃতি ও জলবায়ু	প্রশ্ন ও উত্তর লিংক	বিভিন্ন রোগব্যাধি	প্রশ্ন ও উত্তর লিংক
বিখ্যাত উক্তি	প্রশ্ন ও উত্তর লিংক	পরিমাপক যন্ত্র	প্রশ্ন ও উত্তর লিংক
সংক্ষিপ্ত রূপ বা বিস্তারিত শর্তাবলী	প্রশ্ন ও উত্তর লিংক	রসায়ন	প্রশ্ন ও উত্তর লিংক
আন্তর্জাতিক সংস্থার সংক্ষিপ্ত নাম	প্রশ্ন ও উত্তর লিংক	ভূগোল	প্রশ্ন ও উত্তর লিংক
আন্তর্জাতিক দিবস ও জাতীয় দিবস	প্রশ্ন ও উত্তর লিংক	পদার্থ বিজ্ঞান	প্রশ্ন ও উত্তর লিংক
বিভিন্ন দেশের আয়তন ও রাজধানী	প্রশ্ন ও উত্তর লিংক	জীববিজ্ঞান	প্রশ্ন ও উত্তর লিংক
বিভিন্ন দেশের মুদ্রা নাম	প্রশ্ন ও উত্তর লিংক	গাণিতিক পরিমাপের একক	প্রশ্ন ও উত্তর লিংক
বাংলাদেশের আলােচিত ঘটনাবলী	প্রশ্ন ও উত্তর লিংক	সাধারণ বিজ্ঞান	প্রশ্ন ও উত্তর লিংক
সাম্প্রতিক সোস্যাল মিডিয়া	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

লিখিত পরীক্ষার প্রশ্ন ও সমাধান

গণিত লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	আন্তর্জাতিক বিষয়াবলী লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
বাংলাদেশ লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	বিজ্ঞান ও প্রযুক্তি লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
ইংরেজি লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	মানসিক দক্ষতা লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
বাংলা ১ম ও ২য় পত্র লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক

Paragraph & Composition	উত্তর লিংক	ভাবসম্প্রসারণ, রচনা	উত্তর লিংক
আবেদন পত্র/ Application form	উত্তর লিংক	প্রবন্ধ, অনুচ্ছেদ রচনা	উত্তর লিংক