সূক্ষকোণী ত্রিভূজ কাকে বলে ?, সূক্ষকোণী ত্রিভূজের বৈশিষ্ট্য,সমকোণী ত্রিভূজ কাকে বলে ?,সমকোণী ত্রিভূজ বৈশিষ্ট্য,অতিভূজ কাকে বলে ?, অতিভূজ বৈশিষ্ট্য,স্থুলকোণী ত্রিভূজ কাকে বলে ?,স্থুলকোণী ত্রিভূজ বৈশিষ্ট্য,সমকোণী সমদ্বিবাহু ত্রিভূজ কাকে বলে ?

ত্রিভূজ:
সূক্ষকোণী ত্রিভূজ (Acute angled Triangle):
যে ত্রিভূজের তিনটি কোনই সূক্ষকোণ তাকে সূক্ষকোণী ত্রিভূজ বলে।
পাশের চিত্রে ΔABCΔABC একটি সূক্ষকোণী ত্রিভূজ যার প্রতিটি কোণই
90∘90∘
অপেক্ষা কম।

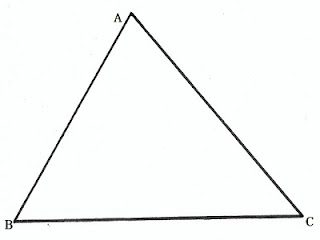
সূক্ষকোণী ত্রিভূজের বৈশিষ্ট্য:
(i) সূক্ষকোণী ত্রিভূজের তিনটি কোনই সূক্ষকোণ অর্থাৎ
90∘90∘
অপেক্ষা কম।
(ii) সমবাহু ত্রিভূজ একটি সূক্ষকোণী ত্রিভূজ যার প্রতিটি কোণ
60∘60∘

সমকোণী ত্রিভূজ (Right angled Triangle):
যে ত্রিভূজের একটি কোণ সমকোণ বা 90∘90∘
এবং বাকী কোণদুটি সূক্ষকোণ অর্থাৎ 90∘90∘
অপেক্ষা কম, তাকে সমকোণী ত্রিভূজ বলে।

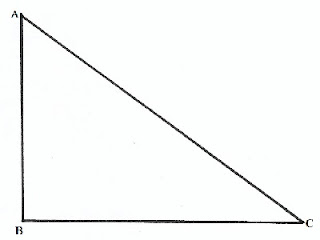
সমকোণী ত্রিভূজের বৈশিষ্ট্য:
(i) সমকোণী ত্রিভূজের একটি কোণ সমকোণ বা 90∘90∘
(ii) সমকোণী ত্রিভূজের বাকী কোণদুটি সূক্ষকোণ।

অতিভূজ (Hypotaneous):
সমকোণী ত্রিভূজের সমকোণের বিপরীত বাহুকে অতিভূজ বলে।
পাশের চিত্রে ΔABCΔABC সমকোণী ত্রিভূজের AC হল অতিভূজ।
অতিভূজ হল যেকোনও সমকোণী ত্রিভূজের বৃহত্তম বাহু।
সমকোণী ত্রিভূজের সমকোণ সংলগ্ন একটি বাহু হল ভূমি এবং অপর বাহুকে লম্ব বলা হয়।
এখানে BC হল ভূমি এবং BA হল লম্ব।

স্থুলকোণী ত্রিভূজ:
যে ত্রিভূজের একটি কোণ স্থুলকোণ অর্থাৎ 90∘90∘
অপেক্ষা বেশী, সেই ত্রিভূজকে স্থুলকোণী ত্রিভূজ বলে।

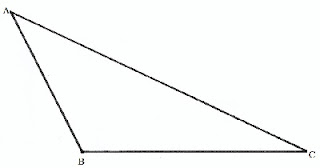
স্থুলকোণী ত্রিভূজের বৈশিষ্ট্য:
(i) স্থুলকোণী ত্রিভূজের একটি কোণ স্থুলকোণ অর্থাৎ 90∘90∘
অপেক্ষা বেশী হয় কিন্তু 180∘180∘
অপেক্ষা কম।
(ii) স্থুলকোণী ত্রিভূজের বাকী কোণদুটি সূক্ষকোণ।

সমকোণী সমদ্বিবাহু ত্রিভূজ (Isosceles right angled triangle):
যে ত্রিভূজের একটি কোণ সমকোণ এবং সমকোণ সংলগ্ন বাহুদুটি পরষ্পর সমান, তাকে সমকোণী সমদ্বিবাহু ত্রিভূজ বলে।
পাশের চিত্রে ΔABCΔABC একটি সমকোণী সমদ্বিবাহু ত্রিভূজ যার ∠ABC=90∘∠ABC=90∘
এবং BA=BCBA=BC।

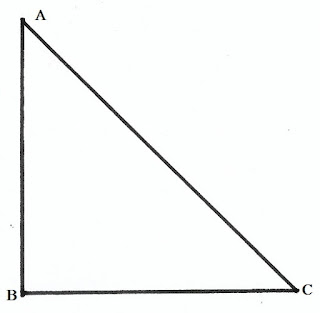
সমকোণী সমদ্বিবাহু ত্রিভূজের বৈশিষ্ট্য:
(i) একটি কোণ সমকোণ।
(ii) সমকোণ সংলগ্ন বাহুদুটি সমান।
(iii) বাকী কোণদুটির মান 45∘45∘।

মধ্যমা (Median):
কোনও ত্রিভূজের যেকোনও শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাকে ওই ত্রিভূজের মধ্যমা বলে।
পাশের চিত্রে ΔABCΔABC ত্রিভূজের AD হল মধ্যমা।

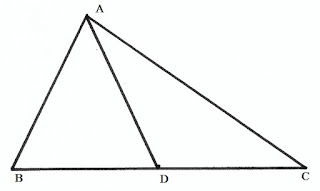
ত্রিভূজের উচ্চতা:
ত্রিভূজের যেকোনও কৌণিক বিন্দু থেকে বিপরীত বাহুর বর্ধিতাংশের উপর অঙ্কিত লম্বকে ওই ত্রিভূজের উচ্চতা বলে।
পাশের চিত্রে ΔABCΔABC ত্রিভূজের AD হল উচ্চতা।

চতুর্ভূজ (Quadrilateral):
চারটি সরলরেখাংশ দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রকে চতুর্ভূজ বলে।
চতুর্ভূজের চারটি বাহু, চারটি শীর্ষবিন্দু ও চারটি কোণ আছে।
চতুর্ভূজ বিষয়ক কয়েকটি তথ্য:
পাশের চিত্রে ABCD একটি চতুর্ভূজ।
(1) এর চারটি বাহু যথাক্রমে AB, BC, CD ও DA
(2) এর চারটি শীর্ষবিন্দু যথাক্রমে A, B, C ও D
(3) এর চারটি কোণ যথাক্রমে
∠DAB∠DAB
∠ABC∠ABC
∠BCD∠BCD
এবং ∠CDA∠CDA
(4) কোনও চতুর্ভূজের দুটি বিপরীত কৌণিক বিন্দুর সংযোজক সরলরেখাকে চতুর্ভূজের কর্ণ বলে।
এখানে ABCD চতুর্ভূজের দুটি কর্ণ যথাক্রমে AC এবং BD
এই কর্ণদুটি একটি বিন্দু O তে ছেদ করে।

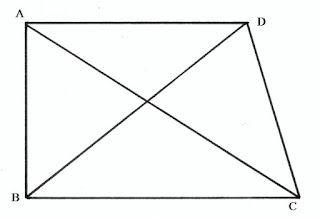
(5) কোনও চতুর্ভূজের যেকোনও শীর্ষবিন্দু সংলগ্ন বাহুদুটিকে সন্নিহিত বাহু বা সংলগ্ন বাহু বলে। কারণ এদের একটি করে সাধারণ শীর্ষবিন্দু আছে।
এখানে ABCD চতুর্ভূজের AD এবং DC বাহুদুটিকে অথবা DC এবং CB বাহুদুটিকে সন্নিহিত বাহু বা সংলগ্ন বাহু বলে।
(6) এখানে ABCD চতুর্ভূজের AD এবং BC অথবা, AB এবং DC বাহুদুটিকে বিপরীত বাহু বলে।
(7) চতুর্ভূজের চারটি কোণের সমষ্টি ∠DAB+∠ABC+∠BCD+∠CDA∠DAB+∠ABC+∠BCD+∠CDA = 360∘360∘
বা চার সমকোণের সমান হয়।
(8) চতুর্ভূজটি সামতলিক ক্ষেত্রের যতটা অংশ স্থান অধিকার করে থাকে, তাকে ওই চতুর্ভূজের ক্ষেত্রফল বলে।
(9) চতুর্ভূজের চারটি বাহুর সমষ্টিকে পরিসীমা বলে।

সামান্তরিক (Parallelogram):
যে চতুর্ভূজের বিপরীত বাহুগুলি সমান ও সমান্তরাল তাকে সামান্তরিক বলে।
এখানে ABCD একটি সামান্তরিক যার AB∥DCAB∥DC এবং AD∥BCAD∥BC আবার AB=DCAB=DC এবং AD=BCAD=BC

সামান্তরিকের বৈশিষ্ট্য:
(i) সামান্তরিকের বিপরীত কোণগুলি সমান এবং চারটি কোণের সমষ্টি 360∘360∘
অথবা 4 সমকোণের সমান।
(ii) সামান্তরিকের কোনও কোনই সমকোণ নয়।
(iii) সামান্তরিকের বিপরীত বাহুগুলি সমান ও সমান্তরাল।
(iv) সামান্তরিকের কর্ণদুটির দৈর্ঘ্য অসমান হলেও তারা পরষ্পরকে সমদ্বিখন্ডিত করে।

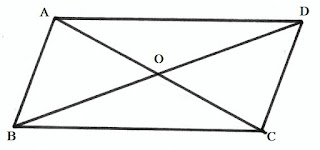
আয়তক্ষেত্র (Rectangle):
যে চতুর্ভূজের বিপরীত বাহুগুলি সমান ও সমান্তরাল এবং প্রত্যেকটি কোণ সমকোণ তাকে আয়তক্ষেত্র বলে।
পাশের চিত্রে ABCD একটি আয়তক্ষেত্র যার AB=DCAB=DC এবং AD=BCAD=BC এবং প্রত্যেকটি কোণ সমকোণ।

আয়তক্ষেত্রের বৈশিষ্ট্য:
(i) আয়তক্ষেত্রের বিপরীত বাহুগুলি সমান ও সমান্তরাল।
(ii) আয়তক্ষেত্রের প্রতিটি কোণ সমকোণ এবং চারটি কোণের সমষ্টি 4 সমকোণ।
(iii) কর্ণদ্বয়ের দৈর্ঘ্য সমান।
(iv) আয়তক্ষেত্রের কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে।

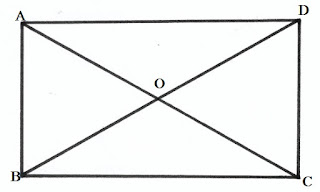
সামান্তরিকের একটি কোণ সমকোণ হলেই, এটি একটি আয়তক্ষেত্র। আয়তক্ষেত্রের শুধুমাত্র একটি কোণ সমকোণ নয়, প্রত্যেকটি কোনই সমকোণ হয়। আয়তক্ষেত্রের কর্ণদুটির দৈর্ঘ্যও সমান হয়। এবং কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে। এছাড়া আয়তক্ষেত্রের বিপরীত বাহুগুলি সমান ও সমান্তরাল। সুতরাং সমস্ত আয়তক্ষেত্রই সামান্তরিক কিন্তু সমস্ত সামান্তরিক আয়তক্ষেত্র নয়।

বর্গক্ষেত্র (Square):
যে চতুর্ভূজের চারটি বাহু সমান এবং প্রতিটি কোণ সমকোণ তাকে বর্গক্ষেত্র বলে।
এখানে ABCD একটি বর্গক্ষেত্র যার AB=BC=CD=DAAB=BC=CD=DA এবং প্রত্যেকটি কোণ সমকোণ।

বর্গক্ষেত্রের বৈশিষ্ট্য:
(i) বর্গক্ষেত্রের চারটি বাহুর দৈর্ঘ্যই সমান।
(ii) বর্গক্ষেত্রের প্রতিটি কোণ 90∘90∘।
(iii) বর্গক্ষেত্রের কর্ণদুটির দৈর্ঘ্য সমান হয়।
(iv) বর্গক্ষেত্রের কর্ণদুটি পরষ্পরকে সমকোণে সমদ্বিখন্ডিত করে।

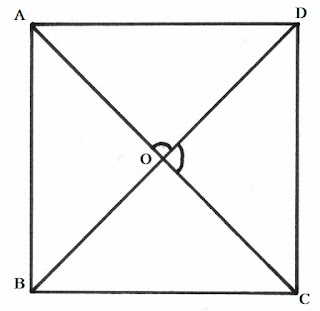
বর্গক্ষেত্রের চারটি বাহুর দৈর্ঘ্যই সমান এবং প্রতিটি কোনই সমকোণ হয়। বর্গক্ষেত্রের কর্ণদুটি পরষ্পর সমান। এবং কর্ণদুটি পরষ্পরকে সমকোণে সমদ্বিখন্ডিত করে, অর্থাৎ কর্ণদুটি পরষ্পরের উপর লম্ব হয়। তাই বলা যায় প্রত্যেক বর্গক্ষেত্রই সামান্তরিক কিন্তু সমস্ত সামান্তরিক বর্গক্ষেত্র নয়।

রম্বস (Rhombus):
যে চতুর্ভূজের চারটি বাহু সমান কিন্তু কোনগুলি সমকোণ নয় তাকে রম্বস বলে।
পাশের চিত্রে ABCD একটি রম্বস যার AB=BC=CD=DAAB=BC=CD=DA কিন্তু কোণগুলি সমকোণ নয়।

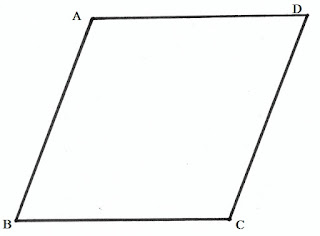
রম্বসের বৈশিষ্ট্য:
(i) রম্বসের চারটি বাহুর দৈর্ঘ্যই সমান।
(ii) রম্বসের কর্ণদুটির দৈর্ঘ্য অসমান।
(iii) রম্বসের কর্ণদুটি পরষ্পরকে সমকোণে সমদ্বিখন্ডিত করে।
(iv) রম্বসের কোণগুলি সমকোণ নয়, কিন্তু চারটি কোণের সমষ্টি 4 সমকোণের সমান।

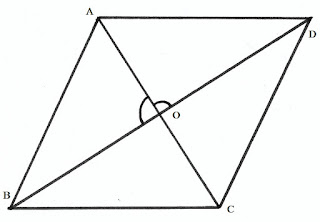
রম্বসের চারটি বাহুর দৈর্ঘ্যই সমান কিন্তু কোণগুলি সমকোণ নয়। এদের কর্ণদুটি পরষ্পর সমান হয় না। কিন্তু কর্ণদুটি পরষ্পরকে সমকোণে সমদ্বিখন্ডিত করে। অর্থাৎ রম্বসের কর্ণদুটি পরষ্পরের ওপর লম্ব। রম্বসের বিপরীত বাহুগুলি সমান্তরাল এবং বিপরীত কোণগুলি পরষ্পর সমান হয়। রম্বসের বাহুসংলগ্ন কোণদুটি পরষ্পর সম্পূরক কোণ। তাই রম্বসও একটি সামান্তরিক। এবং বর্গক্ষেত্র হল রম্বসের একটি বিশেষ রূপ।

ট্রাপিজিয়ম (Trapezium):
যে চতুর্ভূজের কেবলমাত্র একজোড়া বিপরীত বাহু সমান্তরাল কিন্তু তীর্যক বাহু দুটি সমান্তরাল নয়, তাকে ট্রাপিজিয়ম বলে।
পাশের চিত্রে ABCD একটি ট্রাপিজিয়ম যার AB∥CDAB∥CD কিন্তু অপর বিপরীত বাহুদুটি সমান্তরাল নয়।

ট্রাপিজিয়মের বৈশিষ্ট্য:
(i) ট্রাপিজিয়মের দুটি বিপরীত বাহু সমান্তরাল।
(ii) ট্রাপিজিয়মের তীর্যক বাহুদুটি সমান্তরাল নয়।

সমদ্বিবাহু ট্রাপিজিয়াম (Isosceles Trapezium):
যে ট্রাপিজিয়মের তীর্যক বাহুদুটি সমান তাকে সমদ্বিবাহু ট্রাপিজিয়ম বলে।
পাশের চিত্রে ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার তীর্যক বাহু সংলগ্ন কোণ দুটি সমান হবে, অর্থাৎ ∠DAB=∠ABC∠DAB=∠ABC এবং AD=BCAD=BC

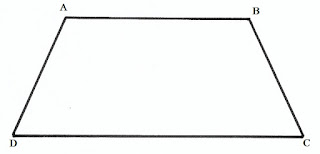
সমদ্বিবাহু ট্রাপিজিয়মের বৈশিষ্ট্য:
(i) সমদ্বিবাহু ট্রাপিজিয়মের যেকোনও সমান্তরাল বাহু সংলগ্ন কোণ দুটি সমান।
(ii) কেবলমাত্র একজোড়া বিপরীত বাহু সমান্তরাল।
(iii) তীর্যক বাহু দুটি সমান্তরাল নয় কিন্তু সমান।

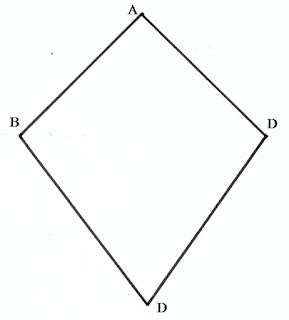
কাইট:
যে চতুর্ভূজের একজোড়া সন্নিহিত বাহুর দৈর্ঘ্য সমান এবং অন্য দুটি সন্নিহিত বাহুর দৈর্ঘ্যও সমান তাকে কাইট বলে।
পাশের চিত্রে ABCD একটি কাইট যার AB=ADAB=AD এবং CB=CDCB=CD

কোনও বহুভূজের কর্ণ সংখ্যা নির্ণয়:
কোনও বহুভূজের বাহুসংখ্যা nn হলে তার কর্ণসংখ্যা হবে =n(n−3)2=n(n−3)2

যেমন:

বহুভূজের নাম	বহুভূজের বাহুসংখ্যা	বহুভূজের কর্ণসংখ্যা
ত্রিভূজ	3	3(3−3)2=03(3−3)2=0
চতুর্ভূজ	4	4(4−3)2=24(4−3)2=2
পঞ্চভূজ	5	5(5−3)2=55(5−3)2=5
ষড়ভূজ	6	6(6−3)2=96(6−3)2=9
অষ্টভূজ	8	8(8−3)2=208(8−3)2=20
দশভূজ	10	10(10−3)2=3510(10−3)2=35

আয়তক্ষেত্র ও ট্রাপিজিয়মের মধ্যে কোন্‌টি সামান্তরিক?
আমরা জানি সামান্তরিকের বিপরীত বাহুগুলি সমান এবং সমান্তরাল। এর বিপরীত কোনগুলিও পরষ্পর সমান হয়।
আয়তক্ষেত্রেও বিপরীত বাহুগুলি সমান ও সমান্তরাল এবং এর চারটি কোনই সমকোণ। তাই বিপরীত কোনগুলিও পরষ্পর সমান হবে। এই কারণে একটি আয়তক্ষেত্রকে সামান্তরিক বলা যেতে পারে।

কিন্তু একটি ট্রাপিজিয়মকে সামান্তরিক বলা যায় না, কারণ এর কেবলমাত্র একজোড়া বিপরীত বাহু সমান্তরাল হলেও সমান হয় না। এবং এর বিপরীত কোণদুটি পরষ্পরের সমান নয়। তাই একটি ট্রাপিজিয়ামকে সামান্তরিক বলা যায় না।

রম্বস ও বর্গক্ষেত্রের মধ্যে কোন্‌টি সুষম চতুর্ভূজ?
বর্গক্ষেত্রের চারটি বাহু সমান এবং কোণগুলিও পরষ্পর সমান। তাই বর্গক্ষেত্র একটি সুষম চতুর্ভূজ। কিন্তু রম্বসের চারটি বাহু সমান হলেও কোনগুলি পরষ্পরের সমান হয় না। তাই রম্বসকে সুষম চতুর্ভূজ বলা যায় না।

সকল রম্বস বর্গক্ষেত্র নয় কেন?
রম্বস ও বর্গক্ষেত্র উভয়েরই বাহুগুলি সমান ও বিপরীত বাহুগুলি সমান্তরাল। কিন্তু
বর্গক্ষেত্রের কোনগুলি সমান হলেও রম্বসের কোণগুলি সমান নয়।
বর্গক্ষেত্রের কর্ণদুটি পরষ্পর সমান কিন্তু রম্বসের কর্ণদুটি পরষ্পর সমান নাও হতে পারে।
তাই সকল বর্গক্ষেত্রই রম্বস কিন্তু সকল রম্বস বর্গক্ষেত্র নয়।

সামান্তরিক	আয়তক্ষেত্র	রম্বস	বর্গক্ষেত্র
বিপরীত বাহু সমান	বিপরীত বাহু সমান	বিপরীত বাহু সমান	বিপরীত বাহু সমান
বিপরীত বাহু সমান্তরাল	বিপরীত বাহু সমান্তরাল	বিপরীত বাহু সমান্তরাল	বিপরীত বাহু সমান্তরাল
বিপরীত কোণ সমান	সব কোণই সমান	বিপরীত কোণ সমান	সব কোনই সমান
কোনও কোণ সমকোণ নয়	প্রত্যেকটি কোণ সমকোণ	কোনও কোণ সমকোণ নয়	প্রত্যেকটি কোণ সমকোণ
কর্ণদুটি সমান নয়	কর্ণদুটি সমান	কর্ণদুটি সমান নয়	কর্ণদুটি সমান
কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে	কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে	কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে	কর্ণদুটি পরষ্পরকে সমদ্বিখন্ডিত করে
কর্ণদুটি পরষ্পরের ওপর লম্ব নয়	কর্ণদুটি পরষ্পরের ওপর লম্ব নয়	কর্ণদুটি পরষ্পরের উপর লম্ব	কর্ণদুটি পরষ্পরের উপর লম্ব

অবস্থানগত দিক থেকে বিভিন্ন প্রকার কোণ ও তাদের সংজ্ঞা:
(1) পূরক কোণ
(2) সম্পূরক কোণ
(3) সন্নিহিত কোণ
(4) বিপ্রতীপ কোণ
(5) একান্তর কোণ
(6) অনুরূপ কোণ
(7) অন্তঃকোণ
(8) অন্তঃস্থ কোণ
(9) বহিঃকোণ

পূরক কোন (Complementary Angle):
দুটি কোণের সমষ্টি এক সমকোণের সমান হলে তাদের একটি কোণকে অপরটির পূরক কোণ বলে।
পাশের চিত্রে ∠AOC∠AOC এবং ∠COB∠COB পরষ্পর পূরক কোণ। অর্থাৎ ∠AOC+∠COB=90∘∠AOC+∠COB=90∘

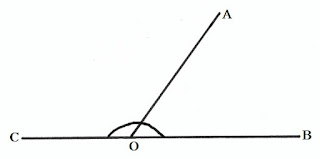
সম্পূরক কোণ (Supplementary Angle):
দুটি কোণের সমষ্টি দুই সমকোণ বা 180∘180∘ হলে তাদের একটিকে অপরটির সম্পূরক কোণ বলে।
পাশের চিত্রে ∠AOB∠AOB এবং ∠AOC∠AOC হল পরষ্পর সম্পূরক কোণ।
অর্থাৎ ∠AOB+∠AOC=∠BOC=180∘∠AOB+∠AOC=∠BOC=180∘

ছেদক বা ভেদক (Transversal):
যে সরলরেখা দুই বা ততোধিক সরলরেখাকে ছেদ করে, তাকে ছেদক বা ভেদক বলে।
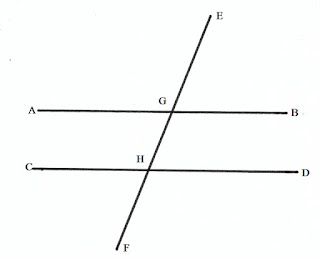
পাশের চিত্রে AB ও CD হল দুটি সরলরেখা এবং EF হল ভেদক বা ছেদক।

একান্তর কোণ (Alternate Angle):
কোনও ছেদক অপর দুটি সরলরেখাকে ছেদ করলে যে আটটি কোণ উৎপন্ন হয়, তার মধ্যে সরলরেখাগুলির মধ্যবর্তী যে কোণগুলি ছেদকের বিপরীত দিকে অবস্থিত এবং পরষ্পর বিপরীত দিকে মুখ করে থাকে, সেই কোনগুলিকে পরষ্পরের একান্তর কোন বলে।
পাশের চিত্রে AB ও CD সরলরেখাদুটির EF ছেদক। এখানে
∠BGH∠BGH ও ∠CHG∠CHG একান্তর কোণ এবং
∠AGH∠AGH ও ∠GHD∠GHD একান্তর কোণ।

অনুরূপ কোন (Similar Angle):
কোনও ছেদক দুটি সরলরেখাকে ছেদ করলে যে আটটি কোণ উৎপন্ন হয়, তার মধ্যে পরষ্পর একই দিকে মুখ করে থাকে সেই কোনগুলিকে অনুরূপ কোণ বলে।
পাশের চিত্রে AB ও CD সরলরেখাদুটির EF ছেদক। এখানে
∠BGE∠BGE এবং ∠DHG∠DHG অনুরূপ কোণ এবং
∠BGH∠BGH এবং ∠DHF∠DHF অনুরূপ কোণ এবং
∠AGE∠AGE এবং ∠CHG∠CHG অনুরূপ কোণ এবং
∠AGH∠AGH এবং ∠CHF∠CHF অনুরূপ কোণ

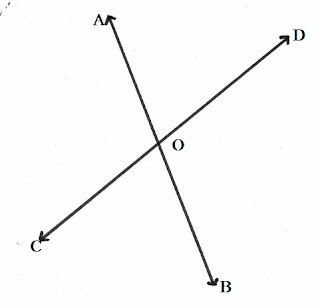
বিপ্রতীপ কোণ (Opposite Angle):
দুটি সরলরেখা পরষ্পরকে ছেদ করলে, ছেদবিন্দুর বিপরীত দিকে যে চারটি কোণের সৃষ্টি করে তাদের মধ্যে পরষ্পর বিপরীত কোন দুটিকে বিপ্রতীপ কোণ বলে।
পাশের চিত্রে AB ও CD সরলরেখা O বিন্দুতে ছেদ করেছে। এখানে
∠AOD∠AOD এবং ∠BOC∠BOC বিপ্রতীপ কোণ এবং
∠AOC∠AOC এবং ∠BOD∠BOD বিপ্রতীপ কোণ

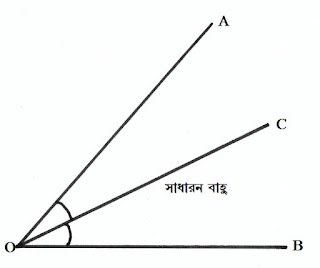
সন্নিহিত কোন (Adjacent Angle):
যদি দুটি কোণের একই শীর্ষ বিন্দু হয় এবং তাদের একটি সাধারণ বাহু থাকে এবং কোণ দুটি ওই সাধারণ বাহুর বিপরীত পার্শ্বে অবস্থান করে, তাহলে ওই কোণদুটিকে সন্নিহিত কোণ বলে।
পাশের চিত্রে ∠AOC∠AOC এবং ∠BOC∠BOC দুটি সন্নিহিত কোণ।

অন্তঃস্থ কোণ:
দুটি সরলরেখাকে একটি সরলরেখা ছেদ করলে যে আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে দুটি সরলরেখার মধ্যবর্তী চারটি কোণকে অন্তঃস্থ কোণ বলে।

অন্তঃকোণ (Interior Angle):
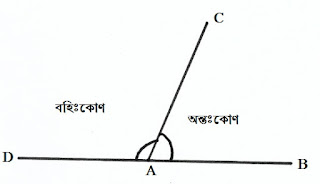
কোণের একটি বাহুকে শীর্ষবিন্দুর দিকে বর্ধিত করলে যে কোণ উৎপন্ন হয়, তাকে বহিঃকোণ বলে। এবং যে কোণের বাহুকে বর্ধিত করা হল তাকে অন্তঃকোণ বলে।
পাশের চিত্রে ∠BAC∠BAC কোণের BA বাহুকে D পর্যন্ত বর্ধিত করায় এখানে
∠CAD∠CAD কোণ হল বহিঃকোণ এবং
∠BAC∠BAC কোণ হল অন্তঃকোণ।

দুটি সরলরেখা সমান্তরাল হওয়ার শর্ত:
দুটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে,
(i) একান্তর কোণ দুটি পরষ্পর সমান হয়।
(ii) অনুরূপ কোণ দুটিও পরষ্পর সমান হয়।
(iii) বিপ্রতীপ কোণ গুলিও পরষ্পর সমান হয়।
(iv) ছেদকের একই পাশে অবস্থিত অন্তঃস্থ কোণ দুটির যোগফল দুই সমকোণের সমান হয়।

আবার উক্তিগুলি বিপরীতক্রমেও সত্য হয়, যথা
(i) দুটি সরলরেখাকে একটি ছেদক ছেদ করলে যদি একান্তর কোণ সমান হয়, তাহলে সরলরেখাদুটি সমান্তরাল হবে।
(ii) দুটি সরলরেখাকে একটি ছেদক ছেদ করলে যদি অনুরূপ কোন গুলি সমান হয়, তাহলে সরলরেখা দুটি সমান্তরাল হবে।

যা যা পড়তে পারেন

১ম থেকে সকল বিসিএস প্রশ্ন ও সমাধান লিংক

Professor Primary Assistant Teacher book লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

ইংরেজি

ইংরেজি ব্যাকরণ

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
Parts of Speech	প্রশ্ন ও উত্তর লিংক	Abbreviations or Elaboration Terms	প্রশ্ন ও উত্তর লিংক
Article	প্রশ্ন ও উত্তর লিংক	One word Substitutions	প্রশ্ন ও উত্তর লিংক
Appropriate Preposition	প্রশ্ন ও উত্তর লিংক	English literature	প্রশ্ন ও উত্তর লিংক
Preposition	প্রশ্ন ও উত্তর লিংক	Sentence Correction	প্রশ্ন ও উত্তর লিংক
Right forms of verb	প্রশ্ন ও উত্তর লিংক	Translation /Vocabulary	প্রশ্ন ও উত্তর লিংক
Voice	প্রশ্ন ও উত্তর লিংক	Spelling	প্রশ্ন ও উত্তর লিংক
Narration	প্রশ্ন ও উত্তর লিংক	Synonym-Antonym	প্রশ্ন ও উত্তর লিংক
Phrase and Idioms	প্রশ্ন ও উত্তর লিংক	Word Meaning	প্রশ্ন ও উত্তর লিংক
prefix and suffix	প্রশ্ন ও উত্তর লিংক	প্রায় ৩০০টি প্রশ্ন উত্তরসহ	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

বাংলা

বিগত ৩০ বছরে বাংলা সাহিত্য ও ব্যাকরণ নিয়োগ পরীক্ষায় আষার সকল MCQ নৈবিত্তিক প্রশ্ন সমাধান এক সাথে, নিয়োগ পরীক্ষায় বাংলা থেকে আসা প্রশ্নগুলোর সমাধান প্রশ্ন ও উত্তর লিংক

বাংলা ব্যাকরণ

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
সন্ধি	প্রশ্ন ও উত্তর লিংক	শেখ হাসিনা	প্রশ্ন ও উত্তর লিংক
বিপরীত শব্দ	প্রশ্ন ও উত্তর লিংক	বঙ্গবন্ধু শেখ মজিবুর রহমান	প্রশ্ন ও উত্তর লিংক
সমার্থক শব্দ	প্রশ্ন ও উত্তর লিংক	জাতীর ৪ নেতা	প্রশ্ন ও উত্তর লিংক
শুদ্ধ বানান	প্রশ্ন ও উত্তর লিংক	বিভিন্ন চুক্তি বাংলাদেশের সাথে ভারতের সীমান্ত	প্রশ্ন ও উত্তর লিংক
এককথায় প্রকাশ	প্রশ্ন ও উত্তর লিংক	মুক্তিযুদ্ধ সেক্টর	প্রশ্ন ও উত্তর লিংক
তৎসম অর্ধতৎসম তদ্ভব বিদেশী ও দেশি শব্দ	প্রশ্ন ও উত্তর লিংক	রােহিঙ্গা সমস্যা	প্রশ্ন ও উত্তর লিংক
উপসর্গ	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের জনপদ	প্রশ্ন ও উত্তর লিংক
সমাস	প্রশ্ন ও উত্তর লিংক	সংবিধান	প্রশ্ন ও উত্তর লিংক
বাগধারা, প্রবাদ ও প্রবচন	প্রশ্ন ও উত্তর লিংক	মুক্তিযুদ্ধ	প্রশ্ন ও উত্তর লিংক
কারক-বিভক্তি	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের ভৌগলিক	প্রশ্ন ও উত্তর লিংক
যুক্ত বর্ণের	প্রশ্ন ও উত্তর লিংক	কবি সাহিত্যিকের রচনা বা জন্ম মৃত্যু	প্রশ্ন ও উত্তর লিংক
ধ্বনি, বর্ণ	প্রশ্ন ও উত্তর লিংক	উপন্যাস/রচনাসমগ্র	প্রশ্ন ও উত্তর লিংক
বাক্য (সরল, জটিল, যৌগিক)	প্রশ্ন ও উত্তর লিংক	ভাষা আন্দোল	প্রশ্ন ও উত্তর লিংক
পদ নির্ণয়	প্রশ্ন ও উত্তর লিংক	বিখ্যাত স্থান	প্রশ্ন ও উত্তর লিংক
দ্বিরুক্ত শব্দ/ দ্বন্দ্ব	প্রশ্ন ও উত্তর লিংক	স্বাধীন বাংলাদেশের অভ্যুদয়ের ইতিহাস	প্রশ্ন ও উত্তর লিংক
বাংলাদেশের চলচ্চিত্র	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের কৃষ্টি ও সংস্কৃতি প্রত্নতাত্ত্বিক নিদর্শন	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

গণিত

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
*দশমিকের (যোগ, বিয়োগ, গুণ, ভাগ)**	প্রশ্ন ও উত্তর লিংক	বীজগাণিতিক মান নির্ণয়	প্রশ্ন ও উত্তর লিংক
শতকরা, লাভ-ক্ষতি, মুনাফা	প্রশ্ন ও উত্তর লিংক	উৎপাদক নির্ণয়, গড়, মধ্যক, প্রচুরক নির্ণয়	প্রশ্ন ও উত্তর লিংক
ল.সা.গু, গ.সা.গু	প্রশ্ন ও উত্তর লিংক	ত্রিভুজক্ষেত্র, বর্গক্ষেত্র	প্রশ্ন ও উত্তর লিংক
ঐকিক নিয়ম (কাজ, খাদ্য, সৈন্য)	প্রশ্ন ও উত্তর লিংক	আয়তক্ষেত্রের বেসিক সূত্রের অংকসমূহ, সরলরেখা	প্রশ্ন ও উত্তর লিংক
অনুপাত:সমানুপাত	প্রশ্ন ও উত্তর লিংক	গাছের উচ্চতা/ মিনারের উচ্চতা	প্রশ্ন ও উত্তর লিংক
সংখ্যা পদ্ধতি	প্রশ্ন ও উত্তর লিংক	মইয়ের দৈর্ঘ্য/সূর্যের উন্নতি	প্রশ্ন ও উত্তর লিংক
বিগত সালে প্রশ্ন	প্রশ্ন ও উত্তর লিংক	পরিমাপ ও পরিমান	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

কম্পিউটার

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
তথ্য ও প্রযুক্তি লিখিত প্রশ্ন উত্তর	প্রশ্ন ও উত্তর লিংক	বাংলাদেশের তথ্য ও যোগাযোগ প্রযুক্তি	প্রশ্ন ও উত্তর লিংক
কম্পিউটার	প্রশ্ন ও উত্তর লিংক	সেটেলাইট-১	প্রশ্ন ও উত্তর লিংক
LAN, WAN কম্পিউটার নেটওয়ার্ক	প্রশ্ন ও উত্তর লিংক	কম্পিউটার সংক্ষিপ্ত শব্দের পূর্ণরুপ	প্রশ্ন ও উত্তর লিংক
গুগল	প্রশ্ন ও উত্তর লিংক	বিভিন্ন দেশের ইন্টারনেট স্পীড	প্রশ্ন ও উত্তর লিংক
৩জি,৪জি, ৫ জি	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

General Knowledge (GK) সাধারণ জ্ঞান ও বিজ্ঞান

প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর	প্রশ্ন	পরীক্ষায় আসার প্রশ্ন ও উত্তর
ইতিহাস , সভ্যতা ও সংস্কৃতি	প্রশ্ন ও উত্তর লিংক	পুরস্কার ও সম্মাননা	প্রশ্ন ও উত্তর লিংক
গভর্নর জেনারেল ও ভাইসরয়দের তালিকা	প্রশ্ন ও উত্তর লিংক	খেলাধুলা	প্রশ্ন ও উত্তর লিংক
বাংলার শাসন আমল	প্রশ্ন ও উত্তর লিংক	জিন-কোষ	প্রশ্ন ও উত্তর লিংক
ভূপ্রকৃতি ও জলবায়ু	প্রশ্ন ও উত্তর লিংক	বিভিন্ন রোগব্যাধি	প্রশ্ন ও উত্তর লিংক
বিখ্যাত উক্তি	প্রশ্ন ও উত্তর লিংক	পরিমাপক যন্ত্র	প্রশ্ন ও উত্তর লিংক
সংক্ষিপ্ত রূপ বা বিস্তারিত শর্তাবলী	প্রশ্ন ও উত্তর লিংক	রসায়ন	প্রশ্ন ও উত্তর লিংক
আন্তর্জাতিক সংস্থার সংক্ষিপ্ত নাম	প্রশ্ন ও উত্তর লিংক	ভূগোল	প্রশ্ন ও উত্তর লিংক
আন্তর্জাতিক দিবস ও জাতীয় দিবস	প্রশ্ন ও উত্তর লিংক	পদার্থ বিজ্ঞান	প্রশ্ন ও উত্তর লিংক
বিভিন্ন দেশের আয়তন ও রাজধানী	প্রশ্ন ও উত্তর লিংক	জীববিজ্ঞান	প্রশ্ন ও উত্তর লিংক
বিভিন্ন দেশের মুদ্রা নাম	প্রশ্ন ও উত্তর লিংক	গাণিতিক পরিমাপের একক	প্রশ্ন ও উত্তর লিংক
বাংলাদেশের আলােচিত ঘটনাবলী	প্রশ্ন ও উত্তর লিংক	সাধারণ বিজ্ঞান	প্রশ্ন ও উত্তর লিংক
সাম্প্রতিক সোস্যাল মিডিয়া	প্রশ্ন ও উত্তর লিংক

নিয়োগ পরীক্ষার নৈবিত্তিক ও লিখিত প্রশ্ন সমাধান লিংক

লিখিত পরীক্ষার প্রশ্ন ও সমাধান

গণিত লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	আন্তর্জাতিক বিষয়াবলী লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
বাংলাদেশ লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	বিজ্ঞান ও প্রযুক্তি লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
ইংরেজি লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক	মানসিক দক্ষতা লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক
বাংলা ১ম ও ২য় পত্র লিখিত পরীক্ষার প্রশ্ন ও সমাধান	সমাধান / উত্তর লিংক

Paragraph & Composition	উত্তর লিংক	ভাবসম্প্রসারণ, রচনা	উত্তর লিংক
আবেদন পত্র/ Application form	উত্তর লিংক	প্রবন্ধ, অনুচ্ছেদ রচনা	উত্তর লিংক