hsc Higher Math 1st Paper suggestion

hsc Higher Math 1st Paper suggestion, Higher Math 1st Paper suggestion pdf, short suggestion hsc Higher Math 1st Paper, Higher Math 1st Paper suggestion hsc, suggestion hsc Higher Math 1st Paper ,

hsc Higher Math 1st Paper suggestion 2026

এইচএসসি উচ্চতর গণিত ১ম পত্র সাজেশন ২০২৬

উচ্চ মাধ্যমিক স্কুল সার্টিফিকেট (এইচএসসি) সুপার সাজেশন ২০২৬ বিজ্ঞান-মানবিক-বাণিজ্য বিভাগ এইচএসসি [ ২০২৬ এর সিলেবাস অনুযায়ী] উচ্চতর গণিত ১ম পত্র (Higher Math 1st Paper) সুপার সাজেশন ২০২৬ subject code: 265

২০২৬ এর এইচএসসি ১০০% কমন সাজেশন

এইচএসসি উচ্চতরগণিত ১ম পত্র সাজেশন,উচ্চতরগণিত ১ম পত্র এইচএসসি সাজেশন, চূড়ান্ত সাজেশন এইচএসসি উচ্চতর গণিত ১ম পত্র, hsc উচ্চতর গণিত ১ম পত্র সাজেশন pdf, এইচএসসি ১০০% কমন উচ্চতর গণিত ১ম পত্র সাজেশন,

এইচএসসি পরীক্ষার সাজেশন ২০২৬ (PDF) লিংক

সর্বশেষ সংশোধিত ও সাজেশন টি আপডেটের করা হয়েছে ২০২৬

উচ্চতর গণিত ১ম পত্র এইচএসসি সাজেশন ২০২৬

কোনাে একটি কলেজের একাদশ শ্রেণির মানবিক, ব্যবসা শিক্ষা ও বিজ্ঞান বিভাগের মােট শিক্ষার্থী সংখ্যা 1500 জন।

কিছু সংখ্যক অনাবাসিক শিক্ষার্থী ব্যতীত অন্যরা M হল ও F হলের আবাসিক শিক্ষার্থী। F হলের 460 জন শিক্ষার্থীর মধ্যে কলেজটির মানবিকের 20%, ব্যবসা শিক্ষার 40% ও বিজ্ঞানের 30% শিক্ষার্থী রয়েছে।

অন্যদিকে M হলের 540 জন শিক্ষার্থীর মধ্যে কলেজের মানবিকের 40%, ব্যবসা শিক্ষার 20% ও বিজ্ঞানের 50% শিক্ষার্থী রয়েছে।

মানবিক, ব্যবসা শিক্ষা ও বিজ্ঞানের শিক্ষার্থী সংখ্যাকে যথাক্রমে x, y ওz দ্বারা প্রকাশ করা হলাে।

শিখনফল/বিষয়বস্তুঃ ম্যাট্রিক্স ও ম্যাট্রিক্সের প্রকারভেদ উদাহরণসহ বর্ণনা করতে পারবে।

ম্যাটিক্স এর সমতা, যোগ, বিয়ােগ ও গুণ করতে পারবে। নির্ণায়কের মান নির্ণয় করতে পারবে। নির্ণয়কের অনুরাশি ও সহগুণক ব্যাখ্যা করতে পারবে। ০ বর্গ ম্যট্রিক্সের বিপরীত ম্যট্রিক্স ব্যাখ্যা করতে পারবে এবং প্রযােজ্য ক্ষেত্রে তা নির্ণয় করতে পারবে।

নির্দেশনা (সংকেত/ধাপ/পরিধি):
ক) তিনটি সমীকরণ গঠন করে AX = B আকারে প্রকাশ কর।

খ) ম্যাট্রিক্সকে A ধরে উহা অভেদঘাতি ম্যাট্রিক্স কিনা যাচাই।

গ) Adj (A) নির্ণয় কর।

ঘ) A + 3A = 21, + 11Y হলে , Y নির্ণয় কর।

ঙ) সমীকরণগুলি সমাধান করে কলেজের মানবিক, ব্যবসা শিক্ষা ও বিজ্ঞান বিভাগের শিক্ষার্থী সংখ্যা নির্ণয় কর।

উত্তর: লিংক

২০২১ সালে একটি কারখানার বিভিন্ন শাখায় কর্মরত শ্রমিকদের তালিকা নিম্নরূপঃ

শাখা	শ্রেণী-১	শ্রেণী-২	শ্রেণী-৩
উৎপাদন	৪	৮	৪
বিপণন	০	৪	৪
বিতরণ	৮	০	৮

ছকের সংখাগুলো একটি ৩*৩ ম্যাট্রিক্স A নির্দেশ করে।  উৎপাদন, বিপণন ও বিতরণ যে শাখাতেই কর্মরত থাকুক না কেন একই শ্রেণীভুক্ত শ্রমিকদের মাসিক বেতন একই।

শিখনফল বা বিষয়বস্তু

ম্যাট্রিক্স ও ম্যাট্রিক্সের প্রকারভেদ উদাহরণসহ বর্ণনা করতে পারবে।

ম্যাট্রিক্স এর সমতা, যোগ, বিয়োগ ও গুণ করতে পারবে।

নির্ণায়কের মান নির্ণয় করতে পারবে।

নির্ণায়ক এর অনুরাশি ও সহগুনক ব্যাখ্যা করতে পারবে।

বর্গ ম্যাট্রিক্স এর বিপরীত ম্যাট্রিক্স ব্যাখ্যা করতে পারবে এবং প্রযোজ্য ক্ষেত্রে তা নির্ণয় করতে পারবে।

নির্ণায়কের সাহায্যে একঘাত সমীকরণ জোটের সমাধান নির্ণয় করতে পারবে।

কাজ :

ক) A ম্যাট্রিক্সটি প্রতিসম কিনা যাচাই কর।

খ) A2-7A+6I3= 2X হলে X নির্ণয় কর।

গ) B=

10 -20 5

10 0 -5

-10 20 5

হলে দেখাও যে,  AB=BA=80I3

ঘ) এমন একটি ম্যাট্রিক্স C নির্ণয় কর যেন AB= CA= I3 হয়।

ঙ) উৎপাদন বিপণন ও বিতরণ শাখার শ্রমিকদের মাসিক বেতন যথাক্রমে 196000 টাকা, 88000 টাকা, 200000 টাকা হলে শ্রেণীর-এক শ্রেণীর-দুই ও শ্রেণি-তিন ভুক্ত একজন শ্রমিকের মাসিক বেতন কত তা নির্ণায়ক এর সাহায্যে নির্ণয় করো।

উত্তর: লিংক

স্থানাঙ্ক জ্যামিতির মাধ্যমে সরলরেখা সংক্রান্ত সমস্যা সমাধান: চিত্রে OABC একটি চতুর্ভুজ। A(-k, 2k), k > 0 এবং OA = 80 একক। oC রেখা, y – 3x = 5 রেখার সমান্তরাল এবং C বিন্দুটি AB এর লম্ব সমদ্বিখণ্ডক রেখার উপর অবস্থিত।

শিখনফলঃ

• দুইটি বিন্দুর মধ্যবর্তী দূরত্ব নির্ণয়ের সূত্র প্রতিষ্ঠা ও প্রয়োগ করতে পারবে। কর
• কোনাে রেখাংশকে নির্দিষ্ট অনুপাতে বিভক্তকারী বিন্দুর স্থানাঙ্ক নির্ণয় করতে পারবে।
• দুইটি বিন্দুর সংযােজক রেখার ঢাল নির্ণয় করতে পারবে।
• অক্ষের সমান্তরাল সরলরেখার সমীকরণ নির্ণয় করতে পারবে।
• অক্ষের সমান্তরাল সরলরেখার সমীকরণ নির্ণয় করতে পারবে।
• বিভিন্ন আকারের সরলরেখার সমীকরণ নির্ণয় করতে পারবে। •দুইটি সরলরেখার ছেদবিন্দু নির্ণয় করতে পারবে।
• বিভিন্ন শর্তাধীনে সরলরেখার সমীকরণ নির্ণয় করতে পারবে।
• সমান্তরাল নয় এমন দুইটি সরলরেখার অর্ন্তভুক্ত কোণ নির্ণয় করতে পারবে।
• কোনাে বিন্দু থেকে একটি সরলরেখার লম্ব দূরত্ব নির্ণয় করতে পারবে।

নির্দেশনাঃ

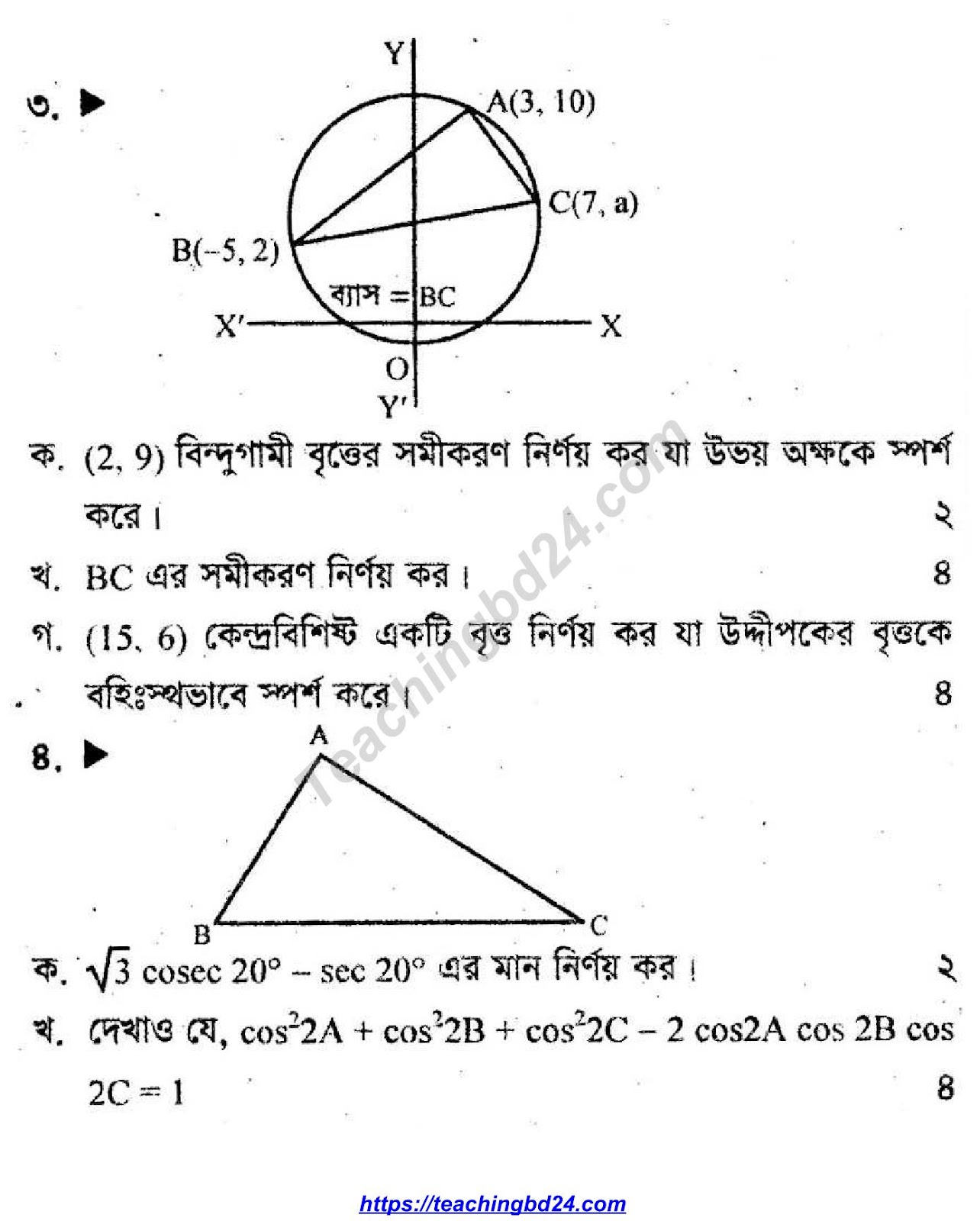
• ক) AB সরলরেখার সমীকরণ নির্ণয় কর।
• খ) C বিন্দুর স্থানাঙ্ক
• গ) ABCD সমকোণী| ত্রিভুজের tan <BCD এর মান নির্ণয় কর।
• ঘ) BD ও BC রেখাদয়ের অন্তর্গত সূক্ষ্মকোণের সমদ্বিখণ্ডকের সমীকরণ নির্ণয় কর।
• ঙ) (1,2) বিন্দু হতে √5 একক দূরবর্তী AB রেখার সমান্তরাল রেখার সমীকরণ নির্ণয় কর।

উত্তর: লিংক

আরো ও সাজেশন:-

Honors Suggestion Links	প্রশ্ন সমাধান সমূহ
Degree Suggestion Links	BCS Exan Solution
HSC Suggestion Links	2016 – 2026 জব পরীক্ষার প্রশ্ন উত্তর
SSC Suggestion Links	বিষয় ভিত্তিক জব পরিক্ষার সাজেশন

উচ্চতর গণিত ১ম পত্র এইচএসসি সুপার সাজেশন pdf download ২০২৬

Chapter 1.1———-12,13,17,19,25,27

Chapter 1.2———– Example 2,5,7(a),9,12,14,15,17,19,20,21,22,26,30,33,34,35(v)

Chapter 3.1———— 10(i), 11(i), 12(i)

Chapter 3.2————-     4(i), 5(ii), 7(iii), 8(ii,iii), 9(v)

Chapter 3.3————–  7, 8(I,iii), 14

Chapter 3.4————–   2(ii), 3

Chapter 3.5- ————-  3(i), 4, 8, 11(i),13(v),15,16,18,19(i),23(i),24, উদাহরণ : 3

Chapter 3.6————–  4(iii), 5(iv,vii), 6(iii), 7(i), 7(iv), 9(iii), 14(i), 15(i), 17(iii),18(i),20(iv)

Chapter 3.7———– 4(iii),    5(ii), 8(iii), 8(viii),10(i), 11(i), 14(iv), 16(ii), উদাহরণ : 2

Chapter 9.1———– 6,12,13,22,24,25(a), 28,33,36,39,40,45,47

Chapter 9.3———–14,27,30,41

Chapter 9.4———–6,17,19,23,28(i),29(i),40,41,43,44,46,47,50(ii),52

Chapter 9.5———–3,4(a), 13,

Chapter 9.6———– 12,13,15,17,20,22,25,27,28,31,35,37

Chapter 9.7———–4,7,9,10,11,13,14,15,17,20

Chapter 9.8———–13,16

Chapter 9.9———– 4,5,12,13,14

Chapter 10.1———–2(iv), 5(ii)

Chapter 10.2———–4(v.,vi,x),5(iv),6(ii)

Chapter  10.3———–2(vii) , 3 (v,vi,vii), 4(vii),5(iii,iv), 7(iv),8(i), 10(iv), 17(i),

Chapter 10.4———– 4(i,ii,iii), 6(iv)

Chapter 10.5———– 2(v),3(ii,iii),5(I,ii),6(I,viii)

Chapter 10.6———–2(I,iv,vii)4(ii),6(vii),7(I,iv), 8(I,iii),9(iii),10(iii),11(I,iii),12(ii),17(i),16(i),15(i),18(ii)

Chapter 10.7———– 4,5(i),6(i),16(ii),20,উদাহরণ :3

pdf download উচ্চতর গণিত ১ম পত্র এইচএসসি সুপার সাজেশন ২০২৬

[ বি:দ্র: উত্তর দাতা: রাকিব হোসেন সজল ©সর্বস্বত্ব সংরক্ষিত (বাংলা নিউজ এক্সপ্রেস)]

২০২৬ উচ্চতর গণিত ১ম পত্র এইচএসসি সাজেশন পিডিএফ ডাউনলোড

মাধ্যমিক ও উচ্চমাধ্যমিক শিক্ষা বোর্ড ঢাকা, চট্টগ্রাম, কুমিল্লা, রাজশাহী, যশোর, বরিশাল,সিলেট দিনাজপুর,বাংলাদেশ কারিগরি শিক্ষা বোর্ড,মাদ্রাসা শিক্ষা বোর্ড, এর কমন সাজেশন ২০২৬

HSC /Alim Common Suggestion 2026

আজকের সাজেশস: ২০২৬ এইচএসসি উচ্চতর গণিত ১ম পত্র পরীক্ষার সাজেশন, ২০২৬ এইচএসসি বর্ষ উচ্চতর গণিত ১ম পত্র সাজেশন,

এইচএসসি উচ্চতর গণিত ১ম পত্র স্পেশাল সাজেশন ২০২৬, hsc Higher Math 1st Paper suggestion 2026

প্রশ্ন ও মতামত জানাতে পারেন আমাদের কে ইমেল : info@banglanewsexpress.com

আমরা আছি নিচের সামাজিক মাধ্যম গুলোতে ও

• Google
• YouTube
• Facebook
• Twitter